UTBK 2023/Penalaran Matematika
Sebuah Gear sepeda digambarkan seperti gambar.

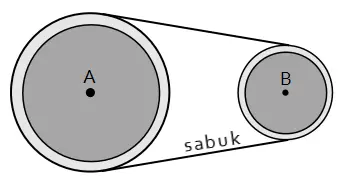
Gear A merupakan gear depan, sedangkan Gear B merupakan gear belakang yang terhubung dengan ban belakang sepeda. Radius Gear A adalah 48 cm, sedangkan radius Gear B adalah 16 cm.

Pertanyaan:

• Soal 1
• Soal 2
• Soal 3
• Soal 4

Soal 1

Jika gear A berputar sebanyak 7 kali, maka gear B berputar sebanyak …. kali.

(A)   ⁷/₃

(B)   7

(C)   14

(D)   21

(E)   Jawaban tidak bisa ditentukan

Jawab: (D)

Dari soal dapat diketahui sebuah gear sepeda digambarkan memiliki ukuran-ukuran berikut.

• Radius Gear A: r_A = 48 cm
• Radius Gear B: r_B = 16 cm
• Perbandingan radius gear A dan B:
  r_A : r_B = 48 : 16 = 3 : 1

Banyak putaran gear sepeda berhubungan dengan kecepatan sudut yaitu seberapa cepat suatu benda berputar atau berputar relatif terhadap titik lain.

Untuk dua buah roda yang dihubungkan oleh sebuah tali, kecepatan linear roda adalah sama. Sedangkan kecepatan sudut dua roda yang dihubungkan oleh sebuah tali memiliki hubungan berbanding terbalik dengan panjang jari-jari.

Banyak putaran gear memiliki hubungan perbandingan senilai dengan kecepatan sudut. Sehingga banyak putaran gear A dan gear B dalam waktu yang sama memiliki hubungan berbanding terbalik dengan radius gear.

Banyak putaran gear A = n_A = 7, banyak putaran gear B = n_B, serta perbandingan radius gear A dan B adalah r_A : r_B = 3 : 1. Cara menghitung banyak putaran gear B dilakukan dengan langkah penyelesaian berikut.

Jadi, jika gear A berputar sebanyak 7 kali maka gear B berputar sebanyak (D) 21 kali.

Soal 2

Tentukan perbandingan kecepatan putaran/kecepatan sudut gear A dan gear B!

(A)   1 : 2

(B)   1 : 3

(C)   2 : 1

(D)   3 : 1

(E)   1 : 1  

Jawab: (B)

Sebuah gear sepeda digambarkan seperti gambar. Terdiri dari gear A dan B merupakan roda yang dihubungkan oleh sebuah tali. Pada teori hubungan roda-roda yang dihubungkan oleh tali memiliki hubungan kecepatan sudut berbanding terbalik dengan jari-jari roda.

Dari soal diketahui bahwa perbandingan radius gear A dan gear B adalah r_A : r_B = 3 : 1. Sehingga, perbandingan kecepatan sudut gear A dan gear B dari sebuah gear sepeda digambarkan seperti gambar ditentukan seperti cara berikut.

Jadi, perbandingan kecepatan putaran/kecepatan sudut gear A dan gear B adalah (B) 1 : 3.

Soal 3

Gear B terhubung dengan ban belakang yang memiliki radius 80 cm. Jika gear A berputar sebanyak 10 kali, maka jarak yang ditempuh adalah … m.

(A) 36π m

(B) 48π m

(C) 72π m

(D) 360π m

(E) 480π m

Jawab: (B)

Dari soal diketahui:

• gear B terhubung dengan ban belakang
• Radius ban belakang: R = 80 cm
• Gear A berputar sebanyak 10 kali

Jarak yang ditempuh sepeda sama dengan hasil kali keliling roda dengan berapa kali roda berputar. Sehingga perlu menghitung berapa banyak putaran yang dilakukan oleh gear belakang sepeda (gear B) terlebih dahulu.

Banyak putaran gear A dan gear B dari sebuah gear sepeda digambarkan seperti gambar memilki hubungan berbanding terbalik dengan perbandingan radius kedua gear. Sehingga banyak putaran gear B saat gear A melakukan 10 kali putaran (n_A = 10) dihitung dengan cara berikut.

Berdasar teori hubungan roda-roda, untuk dua roda yang sepusat memiliki kecepatan sudut yang sama.

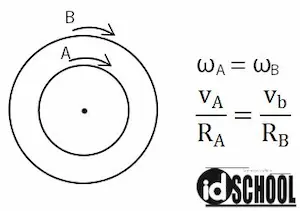
Roda belakang dan gear B memilki poros yang sama sehingga banyak putaran roda belakang = banyak putaran gear B = n_B = 30 kali. Dengan demikian jarak yang ditempuh dapat dihitung seperti cara berikut.

Menghitung jarak yang ditempuh:

Jarak = n × Keliling lingkaran

= 30 × (2π × 80 cm)

= 4.800π cm = 48π m

Jadi, jika gear A berputar sebanyak 10 kali, maka jarak yang ditempuh adalah (B) 48π m.

Soal 4

Jika gear B berputar sebanyak 5 kali dalam 20 s, maka kecepatan sepeda adalah … cm/s.

(A)   20π cm/s

(B)   30π cm/s

(C)   40π cm/s

(D)   50π cm/s

(E)   60π cm/s

Jawab: (C)

Kecepatan sepeda sama dengan jarak yang ditempuh per lamanya waktu tempuh. Dari soal diketahui bahwa waktu tempuh adalah t = 20 s.

Jarak yang ditempuh sepeda dapat dihitung dari banyk putaran roda belakang. Di mana banyak putaran roda belakang sama dengan banyak putaran gear B (hubungan roda-roda sepusat).

Menghitung jarak yang ditempuh sepeda:

Jarak = n × Keliling lingkaran

Jarak = 5 × (2π × 80 cm) = 800π cm

Menentukan kecepatan sepeda (V):

Jadi, jika gear B berputar sebanyak 5 kali dalam 20 s maka kecepatan sepeda adalah (C) 40π cm/s.