UTBK 2023/Pengetahuan Kuantitatif
Perhatikan gambar berikut!

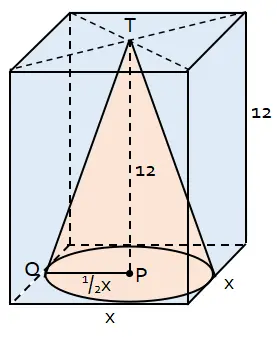
Sebuah kerucut dengan tinggi 12 cm berada di dalam balok yang mempunyai alas persegi. Volume balok di luar kerucut sebesar 100(12 − π) cm³. Berapa luas permukaan kerucut tersebut?
(A) 60π 
(B) 70π 
(C) 80π 
(D) 90π 
(E) 100π 

Jawab: (D)

Dari soal diketahui beberapa informasi berikut.

• Tinggi kerucut: t = 12 cm
• Bentuk alas balok = persegi
• Volume balok di luar kerucut: V₁ = 100(12 − π) cm³

Misalkan panjang sisi persegi alas balok adalah x. Maka jari-jari alas kerucut adalah r = ¹/₂x.

Volume balok di luar kerucut = Volume balok − Volume kerucut

100(12 − π) = 12x² − ¹/₃×π×(¹/₂x²)×12

100(12 − π) = 12x² − πx²

Kita bisa menghilangkan faktor yang sama pada ruas kiri dan kanan.

100(12 − π) = x²(12 − π)

x² = 100

x = √100 = 10 cm

Diperoleh nilai x = 10 cm. Sehingga panjang sisi alas balok adalah 10 cm dan jari-jari alas kerucut adalah r = ¹/₂×10 = 5 cm.

Untuk menghitung luas permukaan kerucut perlu panjang garis pelukis. Yaitu garis TQ yang dapat dihitung menggunakan Teorema Pythagoras.

Menghitung garis pelukis kerucut:

s² = TQ² = TP² + PQ² = 5² + 12²

s² = 25+144 = 169

Sehingga,

s = √169 = 13 cm

Menghitung luas permukaan kerucut:

L = πr(r+s) = π×5×(5+13)

= π×5×18

= 90π cm²

Jadi, luas permukaan kerucut dari sebuah kerucut dengan tinggi 12 cm berada di dalam balok yang mempunyai alas persegi dengan volume balok di luar kerucut sebesar 100(12−π) cm³ adalah L = 90π cm².