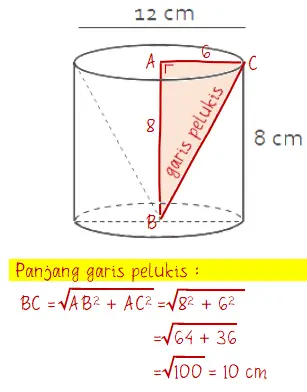
Sebuah kerucut terletak di dalam tabung seperti gambar berikut.

Tentukan perbandingan antara luas permukaan tabung dan kerucut tersebut!
(A) 7 : 3
(B) 7 : 4
(C) 6 : 4
(D) 5 : 4
(E) 4 : 7
Jawab: (B)
Rumus luas permukaan tabung dan kerucut terdapat pada dua persamaan di bawah.
1) Rumus luas tabung:
Ltabung = 2πr(r + t)
2) Rumus luas kerucut:
Lkerucut = πr(r + s)
Berdasarkan informasi pada soal dapat diketahui:
- Jari-jari tabung = jari-jari kerucut = r = 6 cm
- Tinggi kerucut = tinggi tabung = t = 8 cm
Menghitung luas tabung:
Ltabung = 2π6(6 + 8)
Ltabung = 12π × 14 = 168π cm2
Selanjutnya adalah menghitung luas kerucut. Namun nilai s (garis perluki) belum diketahui, sehingga perlu dicari tahu terlebih dahulu. Cara mencari garis pelukis kerucut dapat menggunakan Teorema Pythagoras seperti berikut.
Diperoleh panjang garis pelukis kerucut adalah s = 10 cm. Dengan begitu, luas kerucut sudah bisa dihitung seperti pada cara berikut.
Menghitung luas kerucut:
Lkerucut = π6(6 + 10)
Lkerucut = π6 × 16 = 96π cm2
Jadi, perbandingan antara luas permukaan tabung dan kerucut dari sebuah kerucut terletak di dalam tabung seperti pada gambar tersebut adalah Ltabung : Lkerucut = 168π : 96π = 7 : 4.