UTBK 2023/Penalaran Matematika
Sebuah mesin penggilingan padi dilengkapi dengan dua buah roda A dan B, yang masing-masing beradius 50 cm dan 30 cm. Kedua roda terhubung oleh sebuah sabuk (lihat gambar).

Titik P dan Q masing-masing berada pada permukaan roda, sedangkan P’ dan Q’ berada pada permunkaan sabuk. Pada mulanya, posisi P dan P’ sama, demikian juga dengan posisi Q dan Q’.

Pernyataan:

• Soal 1
• Soal 2
• Soal 3
• Soal 4

Soal 1

Jika jarak P ke Q adalah √39.600 cm, jarak di antara kedua pusat roda adalah … m.

(A)   2

(B)   2,2

(C)   2,5

(D)   3

(E)   3,2

Jawab: (A)

Jarak antara pusat lingkaran, panjang garis singgung persekutuan luar lingkaran, dan selisih jari-jari memenuhi Teorema Pythagoras. Perhatikan gambar sebuah mesin penggilingan padi dilengkapi dengan dua buah roda A dan B berikut.

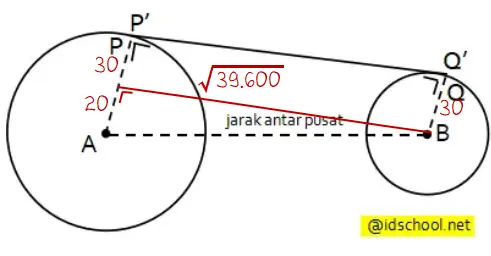
Rumus: AB² = PQ² + (AP – BQ)²

Menghitung jarak di antara kedua pusat roda:

AB² = (√39.600)² + (50 – 30)²

AB² = 39.600 + 20² = 40.000

Sehingga,

AB = √40.000 = 200 cm = 2 m

Jadi, jarak di antara kedua pusat roda adalah AB = 2 m.

Soal 2

Jika roda A sudap berputar sebanyak n kali, maka roda B berputar sebanyak … kali.

Jawab: (C)

Panjang lintasan yang dilalui roda A = panjang lintasan yang dilalui roda B. INGAT!! Panjang lintasan yang dilalui roda sama dengan keliling lingkaran.

Roda A memilik panjang jari-jari r_A = 50 cm dan roda B memiliki panjang jari-jari r_B = 30 cm. Untuk banyak putaran roda A sebanyak n kali, banyak putaran roda B dapat dihitung dengan langkah penyelesaian berikut.

Lintasan roda A = Lintasan roda B

n × Keliling roda A = m × Keliling roda B

Sehingga,

n × 2πr_A = m × 2πr_B

n × 50 = m × 30

Jadi, roda B berputar sebanyak ¹⁰/₆n kali.

Soal 3

Posisi titik P dan Q akan kembali pada posisi semula untuk pertama kalinya saat roda B berputar sebanyak … kali.

(A)   3

(B)   4

(C)   5

(D)   6

(E)   10

Jawab: (A)

Posisi titik P dan Q akan kembali pada posisi semula untuk pertama kalinya ketika jarak yang ditempuh merupakan KPK dari keliling roda A dan B.

Keliling roda A:

K_A = 2×π×r_A

K_A = 2×π×50 = 100π

Keliling roda B:

K_B = 2×π×r_B

K_B = 2×π×30 = 60π

Faktorisasi prima:
60π = 2² × 3 × 5π
40π = 2³ × 5π

KPK = 2³ × 3 × 5π = 8 × 15π = 120π

Sehingga,

Banyak putaran yang dilakukan roda B

Jadi, posisi titik P dan Q akan kembali pada posisi semua untuk pertama kalinya saat roda B berputar sebanyak 3 kali putaran.

Soal 4

Jika jarak antar pusat roda 2 m dan titik P’ bergerak sampai titik Q’, roda A berputar sebanyak … kali.

Jawab: (B)

Saat jarak antar pusat roda 2 m maka panjang lintasan yang dilalui titik P’ yang bergerak sampai titik Q’ adalah √39.600 cm → lihat soal nomor 1

Misalkan banyak putaran roda A adalah n maka lintasan P’ ke Q’ = Keliling roda A × n.

Sehingga,

√39.600 = 2πr_A× n

√39.600 = 2×π×50 × n

Jadi, roda A berputar sebanyak ^√396/_10π kali.