Sebuah pabrik menggunakan bahan A, B, dan C untuk memproduksi 2 jenis barang, yaitu barang jenis I dan barang jenis II. Sebuah barang jenis I memerlukan 1 kg bahan A, 3 kg bahan B, dan 2 kg bahan C. Sedangkan barang jenis II memerlukan 3 kg barang A, 4 kg bahan B, dan 1 kg bahan C.
Harga jenis I adalah Rp40.000,00 dan harga barang jenis II adalah Rp60.000,00 pendapatan maksimum yang diperoleh adalah ….
A. Rp7.200.000,00
B. Rp9.600.000,00
C. Rp10.080.000,00
D. Rp10.560.000,00
E. Rp12.000.000,00
Jawab: D
Masalah soal cerita di atas merupakan topik dari pembahasan program linear. Umumnya, cara menyelesaikan soal cerita program linear meliputi 4 langkah berikut.
- Membuat pemodelan matematika yang sesuai dengan permasalahan.
- Menentukan himpunan penyelesaian yang memenuhi fungsi kendala.
- Menentukan koordinat titik pojok yang membatasi daerah layak yang merupakan himpunan penyelesaian dari fungsi kendala
- Menentukan nilai yang ditanyakan maksimum atau minimum.
Diketahui sebuah pabrik menggunakan bahan A, B, dan C untuk memproduksi 2 jenis barang, yaitu barang jenis I dan barang jenis II. Sehingga pemisalan dapat dilakukan untuk jenis barang I dan II dalam variabel x dan y.
Misalkan:
x = barang jenis I
y = barang jenis II
Tabel di dibawah digunakan untuk membentuk fungsi tujuan dan fungsi kendala dengan lebih mudah.
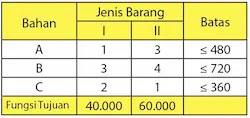
Fungsi tujuan dan fungsi kendala sesuai dengan soal cerita yang diberikan terdapat pada daftar berikut.
Fungsi tujuan:
memaksimalkan f(x, y) = 40.000x + 60.000y
Fungsi kendala:
(i) x + 3y ≤ 480
(ii) 3x + 4y ≤ 720
(iii) 2x + y ≤ 360
(iv) x ≥ 0; (v) y ≥ 0
Daerah layak yang sesuai dengan fungsi kendala:

Dari daerah layak di atas diperoleh lima titik yaitu A, B, C, D, dan E. Kelima titik koordinat dibutuhkan untuk menyelidiki nilai fungsi tujuan f(x, y), sehingga perlu perlu ditentukan terlebih dahulu.
Koorditnat titik A, B, dan E dapat dicari tahu dari diagaram gambar yaitu A(0, 0); B(0, 160); dan E(180, 0). Untuk koordinat titik C dan D perlu dicari tahu dari perpotongan dua garis lurus yang melalui 2 titik.
Menentukan koordinat titik C:
Titik C adalah titik potong antara garis 3x + 4y = 720 dan x + 3y = 480.
Ordinat (y) titik C:
Eliminasi x dari persamaan x + 3y = 480 dan 3x + 4y = 720 untuk mendapatkan nilai y.

Absis (x) titik C:
Susbtitusi nilai y = 144 pada persamaan x + 3y = 480.
x + 3y = 480
x + 3×144 = 480
x + 432 = 480
x = 480 ‒ 432 = 48
Koordinat titik C:
Diperoleh nilai absis titik C adalah x = 46 dan ordinat titik C adalah y = 144. Sehingga titik potong antara garis x + 3y = 480 dan 3x + 4y = 720 adalah C(48, 144).
Menentukan koordinat titik D:
Titik D adalah titik potong antara garis 2x + y = 360 dan 3x + 4y = 720.
Absis (x) titik D:
eliminasi x dari persamaan x + 3y = 480 dan 2x + y = 360 untuk mendapatkan nilai y.
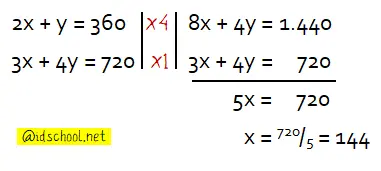
Ordinat (y) titik D:
2x + y = 360
2(144) + y = 360
288 + y = 360
y = 360 ‒ 288 = 72
Koordinat titik D:
Diperoleh nilai absis x = 120 dan ordinat y = 120, maka titik potong antara garis 2x + y = 360 dan 3x + 4y = 720 adalah D(144, 72).
Diperoleh lima titik pojok yaitu A(0, 0); B(0, 160); C(48, 144); D(144, 72); dan E(180, 0). Selanjutnya akan diselidiki nilai fungsi tujuan dengan cara substitusi nilai (x, y) pada fungsi tujuan f(x, y) seperti perhitungan berikut.
| Titik | Fungsi tujuan f(x, y) = 40.000x + 60.000y |
| A(0, 0) | f(0, 0) = 40.000×0 + 60.000×0 = 0 |
| B(0, 160) | f(0, 160) = 40.000×0 + 60.000×160 = 9.600.000 |
| C(48, 144) | f(48, 144) = 40.000×48 + 60.000×144 = 10.560.000 (maks) |
| D(144, 72) | f(120, 120) = 40.000×144 + 60.000×72 = 10.080.000 |
| E(180, 0) | f(180, 0) = 40.000×180 + 60.000×0 = 7.200.000 |
Jadi, untuk sebuah pabrik menggunakan bahan A, B, dan C untuk memproduksi 2 jenis barang maka pendapatan maksimum yang diperoleh adalah Rp10.560.000,00.