UTBK 2019/PK

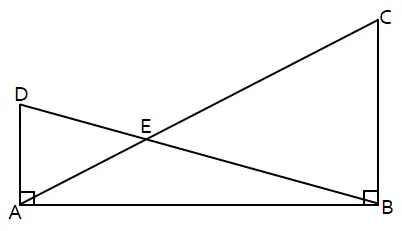
Segilima ABCDE terbentuk dari dua segitiga siku-siku ABC dan BAD dengan AD = 3 dan BC = 5. Sisi AC dan BD berpotongan di titik E. Jika luas △ABE = 12 berpakah jarak E dari AB?

Putuskan apakah pernyataan (1) atau (2) berikut cukup untuk menjawab pertanyaan tersebut.

(1) AC = 14

(2) BD = 12

(A) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.

(B) Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.

(C) DUA Pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.

(D) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, dan pernyataan (2) SAJA cukup.

(E) Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab.

Jawab: (D)

• Dari soal, diketahui:
  • AD = 3
  • BC = 5
  • Luas △ABE = 12

Untuk pernyataan (1) AC = 14:

Misalkan titik F adalah proyeksi titik E ke ruas garis AB. Jarak E dari AB sama dengan panjang ruas garis EF (tinggi segitiga ABE).

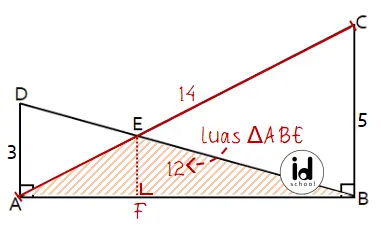
Diketahui panjang ruas garis BC = 5 dan AC = 14 sehingga panjang ruas garis AB dapat dihitung menggunakan Teorema Pythagoras seperti berikut.

Menghitung panjang AB:

AB² = AC² – BC² = 14² – 5²

AB² = 196 – 25 = 171 → AB = √171

Selanjutnya, panjang ruas AB dapat digunakan untuk menghitung EF dengan cara substitusi luas segitiga ABE dan panjang alas AB ke rumus luas segitiga seperti berikut.

Dapat diketahui panjang ruas garis EF. Jadi, pernyataan (1) saja cukup untuk menjawab pertanyaan.

Untuk pernyataan (2) BD = 12:

Misalkan titik F adalah proyeksi titik E ke ruas garis AB. Jarak E dari AB sama dengan panjang ruas garis EF (tinggi segitiga ABE).

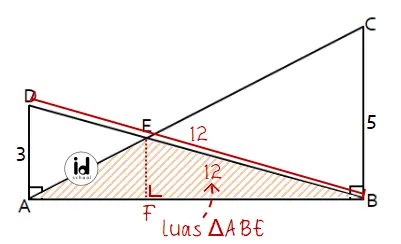
Diketahui panjang ruas garis AD = 3 dan BD = 12 sehingga panjang ruas garis AB dapat dihitung menggunakan Teorema Pythagoras seperti berikut.

Menghitung panjang AB:

AB² = BD² – AD² = 12² – 3²

AB² = 144 – 9 = 135 → AB = √135

Selanjutnya, panjang ruas AB dapat digunakan untuk menghitung EF dengan cara substitusi luas segitiga ABE dan panjang alas AB ke rumus luas segitiga seperti berikut.

Dapat diketahui panjang ruas garis EF. Jadi, pernyataan (2) saja cukup untuk menjawab pertanyaan.

Kesimpulan: Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, dan pernyataan (2) SAJA cukup.