Luas segitiga yang diketahui panjang alas (a) dan tinggi (t) dapat dihitung melalui rumus L = a × t. Sayangnya, pada segitiga sembarang tidak dapat ditentukan mana panjang alas dan tigggi segitiga. Sehingga, luas segitiga sembarang tidak dapat dihitung dengan rumus tersebut. Cara menghitung luas segitiga sembarang dapat menggunakan rumus bentuk lainnya.
Luas segitiga menyatakan besar area yang dibatasi oleh tiga sisi berupa ruas garis lurus yang saling bertemu, antara satu sisi dengan sisi lainnya. Luas segitiga yang diketahui panjang alas dan tinggi dihitung melalui perkalian setengah alas dan tinggi Lantas bagaimana untuk menghitung luas segitiga sembarang yang tidak diketahui mana panjang alas dan tinggi segitiga?

Baca Juga: Rumus Volume Limas dengan Berbagai Bentuk Alas
Pada kasus bentuk segitiga sembarang dapat dilakukan dengan memanfaatkan fungsi trigonometri jika diketahui salah satu besar sudutnya. Luas segitiga sembarang juga dapat dihitung dengan rumus bentuk khusus jika diketahui panjang ketiga sisinya. Bagaimana cara menghitung luas segitga sembarang? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Luas Segitiga Beraturan
Sebelum ke bahasan segitiga tidak beraturan, ingat sedikit mengenai segitiga beraturan. Sebuah segitiga yang diketahui alas dan tingginya secara pasti, luasnya dapat diketahui dengan menghitung setengah dari perkalian alas dan tinggi. Ide mendapatkan rumus ini diperoleh dari bangun segitiga yang diperoleh dari setengah bangun persegi empat.
Perhatikan gambar di bawah.

Terlihat jelas bukan? Bahwa luas daerah segitiga merupakan setengah dari luas persegi. Sehingga, rumus untuk mencari luas segitiga adalah sebagai berikut.

Lalu, bagaimana untuk segitiga yang tidak bisa ditentukan secara pasti antara alas dan tingginya? Segitiga yang tidak dapat diketahui alas dan tingginya secara pasti termasuk dalam bentuk segitiga tidak beraturan.
Cara mencari luas segitiga tidak beraturan dapat diperoleh dengan memanfaatkan fungsi sinus. Selengkapnya dapat disimak pada uraian materi yang lebih jelas pada pembahasan di bawah.
Baca Juga: Jenis – Jenis Segitiga
Luas Seitiga Sembarang
Segitiga sembarang tidak memiliki alas dan tinggi yang diketahui secara pasti. Oleh karenanya, rumus segitiga biasa tidak dapat digunakan di sini. Cara menghitung luas segitiga sembarang dapat memanfaatkan fungsi sinus pada trigonometri jika diketahui besar salah satu sudutnya. Selain itu ada juga bentuk rumus khusus untuk menghitung luas segitiga jika diketahui panjang ketiga sisinya.
Perhatikan gambar sebuah segitiga sembarang di bawah.
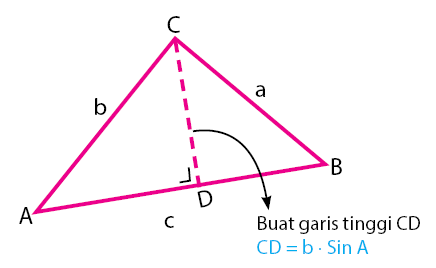
Garis AB pada segitiga ABC pada gambar di atas adalah alas segitiga. Sedangkan tinggi segitiganya adalah CD. Maka, luas segitiga ABC pada gambar dapat dihitung melalui persamaan di bawah.
L∆ABC = ½ × AB × CD
L∆ABC = ½ × c × b ⋅ Sin A
L∆ABC = ½ b c Sin A
Demikianlah, diperoleh persamaan yang yang dapat digunakan untuk menentukan luas segitiga sembarang dengan memanfaatkan fungsi sinus. Dengan mengikuti langkah yang sama, akan diperoleh tiga persamaan berbeda yang dapat digunakan untuk menghitung luas segitiga sembarang.

Berikutnya, jika yang diketahui hanya panjang ketiga sisi segitiga maka rumus luas segitiga sembarang dapat dihitung melalui persamaan berikut.
Sebenarnya, rumus di atas juga dapat digunakan pada segitiga berturan, hanya saja tidak sepraktis jika menggunakan rumus dasar segitga. Berikutnya, akan diberikan contoh soal dan pembahasan terkait cara menghitung luas segitiga sembarang.
Baca Juga: Empat Garis Istimewa Segitiga (Garis Tinggi, Garis Bagi, Garis Berat, Garis Sumbu)
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Luas Segitiga Sembarang

Pembahasan:
Dari gambar yang diberikan pada soal dapat diperoleh panjang segitiga ABC adalah a = 8 cm, b = 6 cm, dan c = 12 cm. Bentuk segitiga yang diberikan tidak dapat diketahui mana panjang dan tinggi segitiga dan ketiga panjangnya diketuhi. Sehingga luas segitiga sembarang tersebut dapat dihitung dengan rumus Heron
Menghitung s:
s = 1/2 × keliling segitiga ABC
s = 1/2 × (8 + 6 + 12)
s = 1/2 × 26 = 13 cm

Jadi, luas segitiga sembarang ABC sama dengan √455 cm2.
Jawaban: C
Baca Juga: Melukis Garis Istimewa Segitiga
Contoh 2 – Soal Luas Segitiga Sembarang
Perhatikan gambar di bawah!

Luas segi enam beraturan yang memiliki jari-jari lingkaran luar 10 cm adalah ….
A. 75√3 cm2
B. 100√3 cm2
C. 125√3 cm2
D. 150√3 cm2
E. 175√3 cm2
Pembahasan:
Penyelesaian soal yang diberikan dapat dengan cara menghitung luas segitiga penyusun segi enam tersebut terlebih dahulu. Perhatikan gambar di bawah!

Menghitung luas sebuah segitiga:
L∆ABC = ½ × AC × BC ⋅ Sin C
L∆ABC = ½ × 10 × 10 ⋅ sin 60o
L∆ABC = ½ × 10 × 10 × ½√3
L∆ABC = 25√3 cm2
Sehingga, luas segi enam tersebut adalah: L = 6 × 25√3 = 150√3 cm2
Jawaban: D
Sekian pembahasan cara mencari luas segitiga sembarang menggunakan fungsi trigonometri, dilengkapi juga dengan contoh soal menggunakan rumus segitiga sembarang beserta pembahasan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Aturan Cosinus( Materi dan Contoh Soal + Pembahasan)

