UTBK 2023/Pengetahuan Kuantitatif
Segitiga PQR dan segitiga STU kongruen.

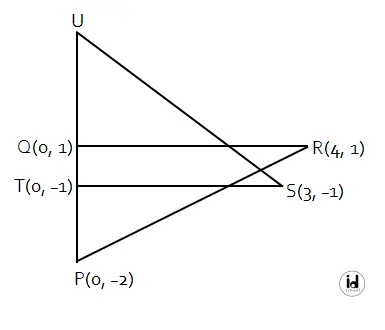
Pertanyaan:

• Soal 1 – Jika (a, b) merupakan koordinat U, nilai a + b adalah ….
• Soal 2 – Luas segitga STU adalah ….

Soal 1 – Jika (a, b) merupakan koordinat U, nilai a + b adalah ….

Jika (a, b) merupakan koordinat U, nilai a + b adalah ….
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6

Jawab: (B)

Titik U(a, b) terletak segaris dengan titik Q, T, dan P. Nilai absis (sumbu-x) dari titik-titik tersebut sama karena segaris. Sehingga absis dari titik U adalah 0, a = 0.

Ordinat (sumbu y) titik U dapat dicari menggunakan kesebangunan.

Perhatikan segitiga PQR dan STU!
Diketahui koordinat titik P, Q, R, S, dan titik T. Sehingga panjang sisi-sisi segitiga yang dibutuhkan dapat dicari.

1) Menghitung panjang PQ:

PQ = √[(0 – 0)² + (1 – (–2))²]

PQ = √[0² + 3²] = √[0 + 9] = √9 = 3

2) Menghitung panjang QR:

QR = √[(4 – 0)² + (1 –  1)²]

QR = √[4² + 0²] = √4² = 4

3) Menghitung panjang ST:

ST = √[(3 – 0)² + (1 – (–1))²]

ST = √[3² + 0²] = √(3² + 0) = √3² = 3

4) Menghitung panjang UT:

UT = √[(0 – 0)² + (b – (–1))²]

UT = √(b + 1)² = b + 1

Diperoleh panjang sisi-sisi segitiga PQR dan segitiga STU pada gambar berikut.

Perbandingan sisi-sisi segitiga pada dua segitiga sebangun merupakan perbandingan senilai. Sehingga dapat dibentuk perbandingan seperti berikut.

b + 1 = 4

b = 4 – 1 = 3

Diperoleh nilai a = 0 dan b = 3. Jadi, nila a + b = 0 + 3 = 3.

Soal 2 – Luas segitga STU adalah ….

Luas segitga STU adalah ….
(A)   12
(B)    9
(C)    6
(D)    4
(E)    3

Jawab: (C)

Rumus luas segitiga adalah LΔ = ¹/₂ × alas × tinggi. Segitiga STU memiliki panjang alas = ruas garis ST dan tinggi segitiga = ruas garis UT.

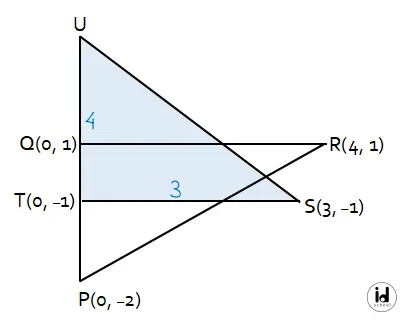
Diketahui panjang ST = 3 dan UT = b + 1 = 3 + 1 = 4. Sehingga, luas segitiga STU dapat dihitung dengan cara berikut.

Menghitung luas segitga STU:

Jadi, luas segitga STU adalah 6 (D).