Semua bilangan real x yang memenuhi |x + 2| + x² > 4 adalah ….
(A)   –2 < x < 1
(B)  x < –2 atau x > 0
(C)  x < –2 atau x > 1
(D)  x < 0 atau x > 1
(E)  x < –2 atau x > 2

Jawab: (C)

Langkah pertama yang perlu dilakukan adalah memindah fungsi ke ruas yang sama sehingga salah satu ruas pertidaksamaan adalah bilangan nol.

Menyederhanakan bentuk pertidaksamaan:

|x + 2| + x² ≥ 4

x² + | x + 2 | – 4 ≥ 0  

Fungsi nilai mutlak f(x) = | x | dapat memiliki dua bentuk persamaan yaitu f(x) = x untuk x > 0 dan f(x) = –x untuk x < 0. Sehingga fungsi f(x) = | x + 2 | dapat memiliki dua bentuk persamaan yaitu f(x) = x + 2 untuk x + 2 ≥ 0 → x ≥ –2 dan f(x) = –(x + 2) untuk x + 2 < 0 → x < –2.

Ada dua persamaan sehingga semua bilangan real x yang memenuhi |x + 2| + x² > 4 adalah gabungan dari dua himpunan penyelesaian yang perlu dicari terlebih dahulu seperti berikut.

1) untuk x ≥ –2:

Bentuk pertidaksamaan menjadi seperti berikut.

x² + x + 2 – 4 > 0

x² + x – 2 > 0

Titik kritis (pembuat nol) tejadi dengan mengambil nilai harga nol yaitu x² + x – 2 = 0. Faktorkan persamaan kuadrat untuk mendapat nilai x yang menjadi titik kritis.

Pemfaktoran:

x² + x – 2 = 0

(x + 2)(x – 1) = 0

x = –2 atau x = 1

Diperoleh dua titik kritis yang membagi garis bilangan menjadi tiga daerah yaitu daerah di kiri -2, antara -2 sampai 1, dan di kanan 1. Ketiga daerah tersebut memiliki nilai positif/negatif yang dapat dicari tahu menggunakan pengujian titik.

Untuk melakukan pengujian titik, ambil sembarang nilai x di salah satu daerah. Misalkan x = 0 kemudian substitusikan ke fungsi f(x) = x² + x – 2. Sehingga f(0) = x² + x – 2 = -2.

Hasil substitusi x = 0 ke fungsi f(x) menghasilkan bilangan negatif. Sehingga daerah yang memuat nilai x = 0 yaitu daerah antara -2 sampai 1 merupakan daerah negatif. Dan dua daerah di samping kiri-kanannya berturut-turut adalah positif.

Di sini terdapat syarat yang harus dipenuhi yaitu x ≥ -2. Sehingga himpunan penyelesaian untuk pertidaksamaan x² + x – 2 ≥ 0 adalah gabungan syarat x ≥ -2 dan daerah positif seperti berikut.

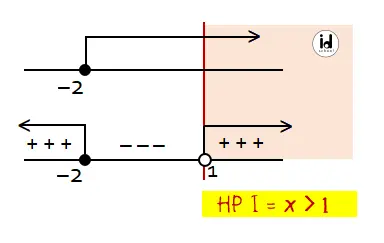
II) untuk x < –2:

Bentuk pertidaksamaan menjadi seperti berikut.

x² – (x + 2) – 4 > 0

x² – x – 2 – 4 > 0

x² – x – 6 > 0

Titik kritis (pembuat nol) tejadi dengan mengambil nilai harga nol yaitu  x² – x – 6 = 0. Faktorkan persamaan kuadrat untuk mendapat nilai x yang menjadi titik kritis.

Pemfaktoran:

x² – x – 6 = 0

(x – 3)(x + 2) = 0

x = 3 atau x = –2

Diperoleh dua titik kritis yang membagi garis bilangan menjadi tiga daerah yaitu daerah di kiri -2, antara -2 sampai 3, dan di kanan 3. Ketiga daerah tersebut memiliki nilai positif/negatif yang dapat dicari tahu menggunakan pengujian titik.

Untuk melakukan pengujian titik, ambil sembarang nilai x di salah satu daerah. Misalkan x = 0 kemudian substitusikan ke fungsi f(x) = x² – x – 6. Sehingga f(0) = 0² – 0 – 6 = -6.

Hasil substitusi x = 0 ke fungsi f(x) menghasilkan bilangan negatif. Sehingga daerah yang memuat nilai x = 0 yaitu daerah antara -2 sampai 3 merupakan daerah negatif. Kemudian dua daerah di samping kiri-kanannya adalah positif.

Di sini terdapat syarat yang harus dipenuhi yaitu x < -2. Sehingga himpunan penyelesaian untuk pertidaksamaan x² + x – 2 ≥ 0 adalah gabungan syarat x < -2 dan daerah positif seperti berikut.

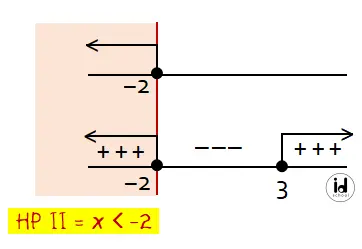
Semua bilangan real x yang memenuhi |x + 2| + x² > 4 adalah gabungan dari HP I = {x > 1} dan HP II = {x < -2}. Jadi, semua bilangan real x yang memenuhi |x + 2| + x² ≥ 4 adalah (C) {x < –2 atau x > 1 }.