Semua bilangan real x yang memenuhi

(A) x < 0
(B) 0 < x ≤ 2
(C) 0 < x < 4
(D) 2 ≤ x ≤ 4
(E) x > 4

Jawab: (C)

Fungsi nilai mutlak f(x) = | x | memiliki dua persamaan yaitu f(x) = x untuk x ≥ 0 dan f(x) = −x untuk x < 0. Sehingga fungsi f(x) = | x – 2 | memiliki dua nilai yaitu f(x) = x – 2 untuk x − 2 x ≥ 0 dan f(x) = -(x – 2) = 2 – x untuk x – 2 < 0.

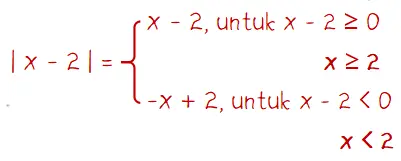
Semua bilangan real x yang memenuhi |x-2|+x/2-|x-2| >= 1 adalah gabungan dari himpunan penyelesaian untuk x ≥ 2 dan himpunan penyelesaian untuk x < 2. Di mana himpunan penyelesaian untuk x ≥ 2 dan x < 2 perlu dicari terlebih dahulu.

Cara menentukan himpunan penyelesaian untuk x ≥ 2 dan x < 2 dilakukan melalui beberapa langkah penyelesaian berikut.

Untuk x ≥ 2:

Nilai mutlak |x − 2| = x − 2 untuk x ≥ 2 sehingga bentuk pertidaksamaannya menjadi seperti berikut.

Samakan penyebutnya sehingga bentuk pertidaksamaan pecahan dapat disederhanakan.

.

.

.

Harga nol pembilang:
3x – 6 = 0
6 – 3x = 6
3x = 6
x = ⁶/₃ = 2

Harga nol penyebut:
-x + 4 = 0
-x = -4
x = ^-4/_-1 = 4

Diperoleh dua nilai x dari harga nol pembilang dan penyebut yaitu x₁ = 2 dan x₁ = 4. Setelah melakukan uji titik dapat diperoleh bahwa daerah yang bernilai positif berada di antara x = 2 dan x = 4.

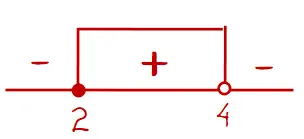
Perlu diperhatikan bahwa di sini terdapat syarat x ≤ 2, sehingga perlu menambahkan syarat tersebut.

Sehingga himpunan penyelesaian dari pertidaksamaan 3x − 6/4 – x ≥ 0 adalah {2 ≤ x < 4}.

Untuk x < 2:

Nilai mutlak |x − 2| = −(x − 2) = 2 − x untuk x < 2 sehingga bentuk pertidaksamaannya menjadi seperti berikut.

.

Samakan penyebutnya sehingga bentuk pertidaksamaan pecahan dapat disederhanakan.

.

Harga nol pembilang:
2 – x = 0
x = 2

Harga nol penyebut: x = 0

Diperoleh dua nilai x dari harga nol pembilang dan penyebut yaitu x₁ = 2 dan x₁ = 0. Setelah melakukan uji titik dapat diperoleh bahwa daerah yang bernilai positif berada di antara x = 0 dan x = 2.

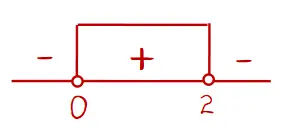
Perlu diperhatikan bahwa di sini terdapat syarat x < 2, sehingga perlu menambahkan syarat tersebut.

Sehingga himpunan penyelesaian dari pertidaksamaan 2 − x/x ≥ 0 adalah {1 < x ≤ 2}.

Diperoleh dua himpunan penyelesaian yaitu HP I = {2 ≤ x < 4} dan HP II = {1 < x ≤ 2}.

Semua bilangan real x yang memenuhi |x-2|+x/2-|x-2| >= 1 adalah gabungan dari HP I dan HP II. Jadi, semua bilangan real x yang memenuhi |x-2|+x/2-|x-2| >= 1 adalah (C) 0 < x < 4.