UTBK 2024
Setengah lingkaran berada di dalam persegi ABCD dengan panjang sisi 8 satuan bersinggungan dengan AB dan CD seperti gambar. Garis E berada di pertengahan AD. EF Menyinggung lingkaran di H dan EG menyinggung lingkaran di I.

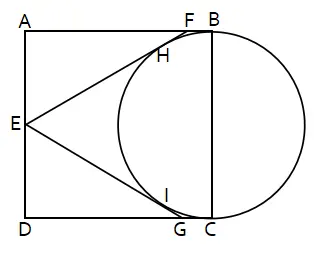
Luas segitiga EHI adalah ….

(A) 8√2

(B) 8√3

(C) 12

(D) 12√2

(E) 12√3

Jawab: (E)

Diketahui setengah lingkaran berada di dalam persegi ABCD. Misalkan O adalah titik pusat lingkaran. Maka jarak titik O ke titik H dan I sama dengan jari-jari lingkaran = setengah sisi persegi = 4 cm.

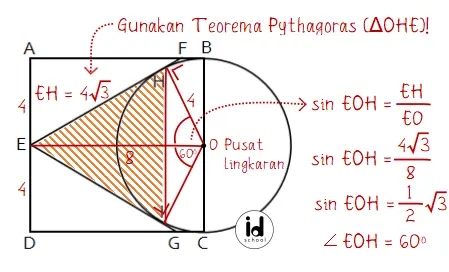
Luas ΔEHI sama dengan luas EHOG dikurangi luas ΔHOI. Sehingga perlu untuk menghitung luas EHOG dan luas ΔHOI terlebih dahulu.

Menghitung luas luas EHOG:

L EHOG = 2 × L ΔEHO

L EHOG = 4 × 4√3 = 16√3 satuan

Menghitung luas luas ΔHOI:

Jadi, L ΔEHI = L EHOG – L ΔHOI = 16√3 – 4√3 = 12√3 satuan.