Seutas tali dipotong menjadi 8 bagian yang panjangnya masing-masing membentuk deret geometri. Apabila tali yang paling pendek adalah 3 cm dan yang terpanjang adalah 384 cm, maka panjang tali semula adalah ….
A. 387 cm
B. 465 cm
C. 486 cm
D. 765 cm
E. 768 cm
Jawab: D
Dari informasi yang diberika pada soal diketahui seutas tali dipotong menjadi 8 bagian yang panjangnya membentuk deret geometri. Selain itu diketahui juga panjang potongan tali terpendek dan terpanjang.
- Panjang tali terpendek: U1 = a = 3 cm
- Panjang tali terpanjang: U8 = 384 cm
Untuk mengetahui panjang tali lain perlu rumus Un dari deret geometri tersebut. Rumus suku ke-n (Un) dan jumlah n suku pertama (Sn) dari suatu deret geometri terdapat pada persamaan berikut.
- Suku ke-n: Un = arn-1
- Jumlah n suku pertama:
Substitusi nilai U1 = a = 3 cm pada U8 = ar7 = 384 cm untuk menentukan nilai rasio (r) dari deret geometri yang dibentuk potongan tali tersebut.
Mencari rasio (r):
U8 = ar7 = 384
3 × r7 = 384
r7 = 384/3 = 128
r = 7√128 = 2
Diketahui suku pertama a = 3 dan rasio r = 2. Nilai a dan r dari deret geomerti dapat digunakan untuk mencari jumlah n suku pertama deret tersebut.
Panjang tali semula dari seutas tali dipotong menjadi 8 bagian yang panjangnya masing-masing membentuk deret geometri sama dengan jumlah 8 suku pertama deret geomteri (S8) dengan a = 3 dan r = 2,
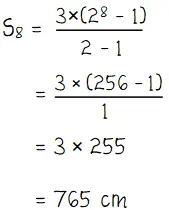
Jadi, panjang tali semula dari seutas tali dipotong menjadi 8 bagian yang panjangnya masing-masing membentuk deret geometri adalah S8 = 765 cm.