Bentuk kurva permintaan dan penawaran berupa garis lurus dengan suatu kemiringan. Ukuran kemiringan garis dari kurva permintaan dan penawaran disebut gradien atau slope. Kurva permintaan selalu condong ke kiri sehingga memiliki nilai gradien yang negatif (b < 0). Sementara kurva penawaran condong ke kanan sehingga memiliki nilai gradien yang positif (b > 0).
Bentuk umum persamaan fungsi permintaan dan penawaran adalah Q = a + bP. Dari persamaan tersebut yang menjadi ukuran kemiringan garis adalah koefisien di depan Y. Sedangkan untuk bentuk persamaan P = a + bQ, ukuran kemiringan garis adalah koefisien di depan Q. Atau, nilai kemiringan garis pada bentuk umum fungsi permintaan dan penawaran adalah nilai b.
Nilai kemiringan garis yang semakin tinggi menunjukkan bahwa garis semakin tegak (vertikal). Sedangkan untuk ukuran kemiringan garis yang semakin rendah menunjukkan bahwa garis semakin mendatar (horizontal).
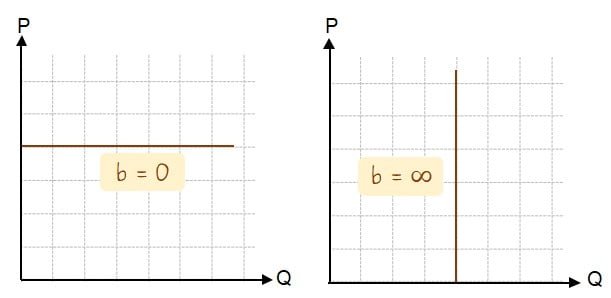
Untuk nilai b = 0 maka bentuk kurva permintaan dan penawaran berupa garis lurus mendatar (horizontal). Sedangkan untuk nila b = ∞ maka bentuk kurva permintaan dan penawaran berupa garis tegak atau vertikal.
Baca Juga: Rumus Fungsi Penawaran dan Permintaan
Bentuk kurva permintaan dan penawaran digambar berdasarkan fungsi permintaan atau penawaran. Bagaimana cara menggambar kurva permintaan dan penawaran? Bagaimana cara menentukan persamaan yang sesuai dengan kurva permintaan dan penawaran? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Cara Menggambar Kurva Permintaan
- Cara Menggambar Kurva Penawaran
- Gabungan Kurva Permintaan dan Penawaran
- Contoh Soal dan Pembahasan
Cara Menggambar Kurva Permintaan
Kurva permintaan memiliki karakteristik nilai gradien kurang dari nol (b < 0) atau kurva condong ke kiri. Bentuk umum persamaan fungsi permintaan dapat berupa Q = a ‒ bP atau P = a ‒ bQ. Cara menggambar kurva permintaan dapat dilakukan melalui beberapa langkah berikut.
- Amati data yang diberikan
- Persiapkan bidang gambar berupa bidang koordinat dengan sumbu x dan sumbu y
- Gunakan sumbu x untuk jumlah (Q) dan sumbu y untuk harga (P)
- Pasangkan titik-titik harga dan jumlah yang sesuai pada titik koordinat (Q, P)
- Hubungkan titik-titik yang diperoleh sehingga terbentuk sebuah garis lurus
- Diperoleh bentuk kurva berupa garis lurus yang condong ke kiri
Untuk menambah pemahaman sobat idschool mengenai bagaimana cara menggambar kurva permintaan melalui contoh menggunakan data berikut.
| Harga (P) | Jumlah (Q) |
| 4.000 | 90 |
| 5.000 | 80 |
| 6.000 | 70 |
| 7.000 | 60 |
| 8.000 | 50 |
| 9.000 | 40 |
| 10.000 | 30 |
Pertama, sobat idschool perlu membuat bidang koordinat dengan ukuran menyesuaikan data yang diketahui. Selanjutnya sobat idschool perlu menentukan titik-titik koordinat yang sesuai. Terakhir, hubungkan titik-titik koordinat tersebut sehingga diperoleh sebuah garis lurus condong ke kiri yang merupakan bentuk kurva permintaan.

Baca Juga: Rumus Fungsi Konsumsim (C) dan Fungsi Tabungan (S)
Cara Menggambar Kurva Penawaran
Kurva penawaran memiliki karakteristik nilai gradien lebih dari nol (b > 0) atau kurva condong ke kanan. Bentuk umum persamaan fungsi permintaan dapat berupa Q = a + bP atau P = a + bQ. Cara menggambar kurva penawaran dapat dilakukan melalui beberapa langkah berikut.
- Amati data yang diberikan
- Persiapkan bidang gambar berupa bidang koordinat dengan sumbu x dan sumbu y
- Gunakan sumbu x untuk jumlah (Q) dan sumbu y untuk harga (P)
- Pasangkan titik-titik harga dan jumlah yang sesuai pada titik koordinat (Q, P)
- Hubungkan titik-titik yang diperoleh sehingga terbentuk sebuah garis lurus
- Diperoleh bentuk kurva berupa garis lurus yang condong ke kanan
Untuk menambah pemahaman sobat idschool mengenai bagaimana cara menggambar kurva penawaran melalui contoh data berikut.
| Harga (P) | Jumlah (Q) |
| 4.000 | 30 |
| 5.000 | 40 |
| 6.000 | 50 |
| 7.000 | 60 |
| 8.000 | 70 |
| 9.000 | 80 |
| 10.000 | 90 |
Pertama, sobat idschool perlu membuat bidang koordinat dengan ukuran menyesuaikan data yang diketahui. Selanjutnya sobat idschool perlu menentukan titik-titik koordinat yang sesuai. Terakhir, hubungkan titik-titik koordinat tersebut sehingga diperoleh sebuah garis lurus condong ke kanan yang merupakan bentuk kurva penawaran.

Baca Juga: Cara Menentukan Jenis Inflasi dengan Indeks Harga Agregatif Sederhana
Gabungan Kurva Permintaan dan Penawaran
Antara kurva permintaan dan penawaran dapat digambarkan dalam sebuah bidang koordniat. Kurva permintaan dan penawaran yang digambarkan dalam satu bidang dapat memiliki sebuh titik potong. Titik potong antara kurva permintaan dan penawaran disebut titik ekuilibrium.

Titik ekuilibrium adalah kondisi di mana banyak permintaan sama dengan banyak penawaran, sehingga titik ekuilibrium disebut titik keseimbangan pasar. Letak titik ekuilibrium dapat diperoleh dengan mengambil persamaan fungsi permintaan dan fungsi penawaran.
Baca Juga: Pengaruh Subsidi dan Pajak Terhadap Letak Titik Keseimbangan Pasar
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana penggunaan kurva permintaan dan penawaran. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Kurva Permintaan dan Penawaran
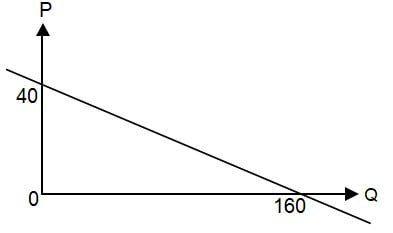
Berdasarkan kurva permintaan di atas, fungsi permintaan kurva yang sesuai adalah ….
A. P = 2Q + 20
B. P = ‒0,5Q + 20
C. P = ‒¼Q + 40
D. P = ¼Q + 10
E. P = ‒¼Q + 20
Pembahasan:
Dari kurva yang diberikan dapat diketahui dua titik yang dilalui kurva yaitu (160, 0) dan (0, 40). Dari dua titik tesebut dapat diperoleh nilai P1 = 0, Q1 = 160, P2 = 40, dan Q2 = 0. Sehingga persamaan fungsi permintaan dapat ditentukan melalui cara berikut.

Jadi, fungsi permintaan dari kurva tersebut adalah P = 1/4Q ‒ 40.
Jawaban: C
Contoh 2 – Soal Kurva Permintaan dan Penawaran
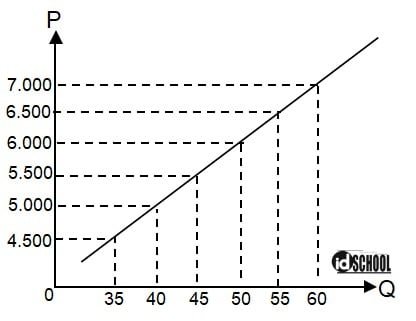
Berdasarkan kurva penawaran beras di atas, maka fungsi penawaran yang tepat adalah ….
A. P = 100Q + 1.000
B. P = 100Q ‒ 1.000
C. P = ‒100Q + 1.000
D. Q = 100P + 1.000
E. Q = 100P ‒ 1.000
Pembahasan:
Berdasarkan kurva yang diberikan dapat diketahui enam titik koordinat yang dilalui kurva. Dari enam titik koordinat tersebut ambil dua titik, misalnya (40, 5.000) dan (50, 6.000). Dari dua titik yang dipilih memuat dua nilai P dan dua nilai Q seperti berikut.
- (40, 5.000) → Q1 = 40 dan P1 = 5.000
- (50, 6.000) → Q2 = 50 dan P2 = 6.000
Menentukan fungsi penawaran:
P ‒ P1/P2 ‒ P1 = Q ‒ Q1/Q2 ‒ Q1
P ‒ 5.000/6.000 ‒ 5.000 = Q ‒ 40/50 ‒ 40
P ‒ 5.000/1.000 = Q ‒ 40/10 *kali silang
10(P ‒ 5.000) = 1.000(Q ‒ 40)
10P ‒ 50.000 = 1.000Q ‒ 40.000
10P = 1.000Q ‒ 40.000 + 50.000
10P = 1.000Q + 10.000 (*kedua ruas dibagi 10)
P = 100Q + 1.000
Jadi, fungsi penawaran yang tepat adalah P = 100Q + 1.000
Jawaban: A
Demikianlah tadi ulasan bagaimana cara menggambar kurva permintaan dan penawaran beserta contohnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Rumus Koefisien Elastisitas (5) dan Contoh Cara Menghitungnya
