Pengertian limit, secara bahasa dapat diartikan sebagai ambang batas. Misalnya, sebuah kartu kredit memiliki limit Rp5.000.000,00. Artinya, kartu kredit tersebut mempunyai ambang batas Rp5.000.000,00. Begitu juga untuk pengertian limit secara matematika, limit dalam matematika juga dapat diartikan sebagai batas yang dapat dicapai di suatu titik. Melalui halaman ini, idschool akan mengulas tentang apa itu pengertian limit dan bagaimana cara menentukan nilainya.
Dalam matematika, nilai limit dapat dikatakan sebagai prediksi nilai ordinat yang didapat pada suatu titik. Nilai limit diperoleh dengan pendekatan dari sisi kanan dan sisi kiri. Jika nilai limit dari kiri sama dengan nilai limit dari kanan maka fungsi f(x) mempunyai nilai limit. Notasi limit dismibolkan pada persamaan di bawah.

Cara membaca notasi limit di atas adalah nilai limit f(x) untuk x mendekati a dinyatakan dalam sebuah nilai yang terletak pada ordinat (y).
Penjelasan mengenai pengertian limit dan cara menentukan nilainya dapat lebih banyak dicari tahu melalui ulasan pengertian limit di bawah.
Table of Contents
Nilai Limit Terdefinisi di Semua Titik
Bagaimana cara mencari nilai limit?
Nilai limit diperoleh melalui pendekatan dari kiri dan kanan. Secara sederhana, limit dapat diartikan sebagai nilai y yang merupakan prediksi dari nilai suatu fungsi di suatu titik.
Ulasan pertama yang akan dibahas adalah menentukan nilai limit pada grafik linear melalui pengertian limit. Seperti kita tahu bahwa grafik linear terdefinisi di semua titik seperti yang terdapat pada grafik fungsi linear di bawah.
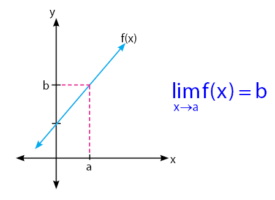
Berdasarkan grafik di atas, nilai x terdefinisi di semua titik. Nilai limit f(x) untuk x mendekati a dari kanan adalah b dan nilai limit f(x) untuk x mendektai a dari kiri adalah b. Sehingga, kesimpulan yang dapat diambil adalah nilai limit f(x) adalah b.
Contoh kasus pertama ini merupakan kasus sederhana tentang limit karena diberikan grafik linear yang nilai x terdefinisi di semua titik.
Pada pembahasan pengertian limit, kita tidak melihat apa yang terjadi pada satu titik, tapi melihat nilai yang dapat terjadi di sekitar titik ketika didekati sangat dekat dari kiri dan dari kanan. Kondisi tertentu dapat memungkinkan grafik yang nilai x tidak terdefinisi di suatu titik. Namun, tidak mustahil jika nilai limitnya sama dengan grafik yang terdefinisi di semua titik.
Untuk lebih jelasnya, perhatikan grafik yang diberikan pada gambar di bawah.

Grafik di atas tidak terdefinisi pada titik x = a. Namun, ketika fungsi f(x) didekati dari kiri, nilainya akan menuju titik b. Begitu juga ketika f(x) didekati dari kanan, nilainya akan menuju titik b. Kesimpulannya, nilai limit f(x) adalah b.

Sebagian orang mungkin menanyakan, mengapa jika nilai limit merupakan nilai yang diperoleh dari pendekataan, notasi limit disimbolkan dengan tanda sama dengan?
Hal ini dikarenakan penyimbolan limit memang dibuat seperti demikian. Ini merupakan simbol notasi limit, tidak ada alasan lain.
Sekarang, idschool akan menujukkan kasus fungsi yang tidak memiliki limit.
Nilai Llimit Tidak Ada
Ada sebuah kondisi tertentu, di mana nilai limit f(x) yang didekati dari kiri tidak sama dengan nilai limit yang didekati dari kanan. Kondisi ini tentunya tidak akan menghasilkan nilai limit. Untuk lebih jelasnya, perhatikan grafik di bawah.

Untuk mendapatkan nilai limit f(x) di titik x = a, sobat idschool perlu mencari tahu nilai limit f(x) jika x didekati dari kiri dan kanan. Selanjutnya, sobat idschool perlu membandingkan nilai limit f(x) untuk x mendekati a dari kiri dan untuk x mendekati a dari kanan.
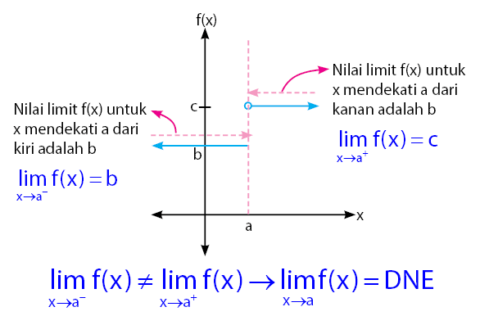
Berdasarkan grafik yang diberikan di atas, untuk x mendekati a dari kiri, nilai limitnya adalah b, sedangkan untuk x mendekati a dari kanan, nilai limitnya adalah c.
Kita mendapatkan nilai limit f(x) untuk x mendekati a dari kiri tidak sama dengan nilai limit f(x) untuk x mendekati a dari kanan. Kesimpulanya, nilai limit f(x) tidak ada, biasa ditulis dengan DNE (Do Not Exist).
Selanjutnya, ulasan kasus yang ke tiga adalah nilai limit untuk x mendekati tak hingga (x → ∞) dan x mendekati negatif tak hingga (x → ‒∞).
Nilai Limit di Tak Hingga
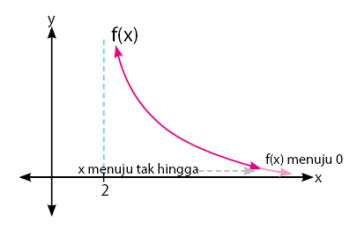
Ulasan yang akan dibahas di sini adalah cara menentukan nilai limit fungsi jika x mendekati tak hingga. Untuk mengetahui caranya, perhatikan gambar grafik fungsi f(x) dan g(x) yang diberikan di bawah.

Nilai limit f(x) untuk x mendekati tak hingga, nilainya adalah 0. Hasil ini diperoleh dengan mendekati nillai f(x) ketika x mendekati tak hingga, grafik akan menuju titik 0. Perhatikan grafik di bawah.
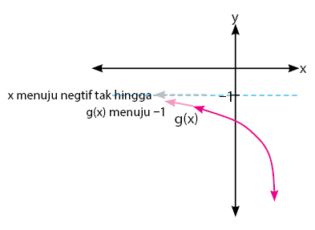
Hampir sama seperti cara di atas, nilai limit g(x) untuk x mendekati negatif tak hingga, nilainya adalah ‒1. Hasil ini diperoleh dengan mendekati nillai f(x) ketika x mendekati negatif tak hingga, grafik akan menuju titik ‒1. Perhatikan grafik di bawah.
Sekian pembahasan mengenai pengertian limit. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga:7 Tips Menyelesaikan Soal Limit Fungsi di Suatu Titik
