Suku ketiga suatu barisan aritmatika adalah 22. Jika jumlah suku ketujuh dan suku ke sepuluh

Suku ketiga suatu barisan aritmatika adalah 22. Jika jumlah suku ketujuh dan suku ke sepuluh adalah 0, maka jumlah lima suku pertama sama dengan ….
A. 30
B. 60
C. 85
D. 110
E. 220

Jawab: D

Pada soal diketahui bentuk barisan merupakan barisan aritmatika. Sehingga rumus suku ke-n dan jumlah n suku pertama menggunakan persamana berikut.

• Suku ke-n: Un = a + (n − 1)b
• Jumlah n suku pertama:

Keterangan:
a = suku pertama barisan
b = beda barisan
n = bilangan asli (n = 1, 2, 3, ….)

Berdasarkan keterangan pada soal dapat diperoleh beberapa informasi berikut.

• Suku ketiga suatu barisan aritmatika adalah 22
  U₃ = 22 → a + 2b = 22

• Suku ketujuh + suku ke sepuluh = 0: maka jumlah
  U₇ + U₁₀ = 0
  (a + 6b) + (a + 9b) = 0
  2a + 15b = 0

Diperoleh dua persamaan yaitu (i) a + 2b = 22 dan (ii) 2a + 15b = 0. Nilai a dan b dapat diketahui dengan menyelesaikan sistem persamaan linear dua variabel (SPLDV) dari (i) dan (ii).

Menentukan nilai b:
Eliminasi a dari persamaan (i) dan (ii) untuk mendapat b seperti cara berikut.

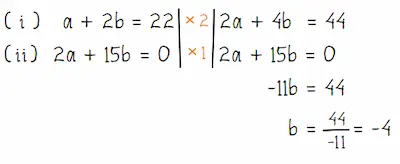
Menentukan nilai a:
Substitusi nilai b = −4 pada persamaan (i) a + 2b = 22 untuk mendapat nilai a.

a + 2b = 22
a + 2×(−4) = 22
a − 8 = 22
a = 22+8 = 30

Diperoleh nila a= 30 dan b = −4 yang dapat digunakan untuk menentukan jumlah 5 suku pertama barisan aritmatika tersebut. Cara menentukan jumlah 5 suku pertama terdapat pada perhitungan berikut.

Menghitung jumlah 5 suku pertama:
S₅ = ⁵/₂(2×30 + 4×(−4 ))
S₅ = ⁵/₂(60−16)
S₅ = ⁵/₂×44 = 110

Jadi, jumlah lima suku pertama sama dengan S₅ = 110.