UTBK 2024/Penalaran Matematika (PM)
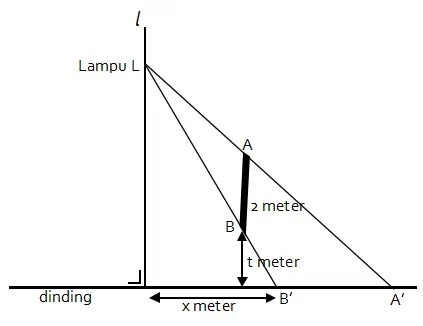
Titik A dan B terletak pada dua ujung suatu tembok tetap yang sejajar dengan garis l dan tegak lurus dengan dinding. Jarak titik A dan B adalah 2 meter. Lampu L terletak pada garis l sehingga bayangan titik A dan B, yaitu A’ dan B’ terletak pada dinding.

Pertanyaan:

• Soal 1
• Soal 2
• Soal 3
• Soal 4

Soal 1

Jika t = 2 dan x = 3, dan jarak titik A’ ke garis l adalah 6 meter,  jarak lampu L ke dinding adalah … meter.
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8

Jawab: (E)

Misalkan jarak lampu ke dinding adalah d meter, titik O adalah titik perpotongan garis l dengan dinding, dan titik P adalah proyeksi titik A ke dinding. Diketahui jarak titik A’ ke garis l = 6 meter dan panjang x = 3 meter, maka jarak titik P ke titik A’ adalah PA’ = 6 – 3 = 3 meter.

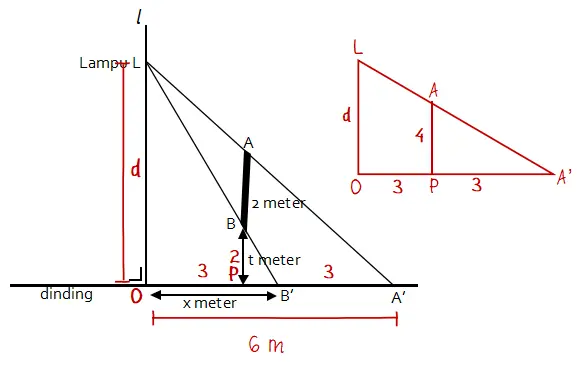
Selanjutnya, nilai d dapat dicari menggunakan kesebangunan segitiga A’OL dan segitiga A’PA.

Soal 2

Diketahui t  2 dan x = 2, dan panjang bayangan dinding AB pada dinding adalah 3 meter. Jadi, jarak lampu ke dinding adalah … meter.
(A) 5
(B) 4√2
(C) 6
(D) 7
(E) 5√2

Jawab: (C)

Misalkan jarak lampu ke dinding adalah d meter, perpotongan garis l dan dinding adalah titik O, dan proyeksi titik A dan B pada dinding adalah P.

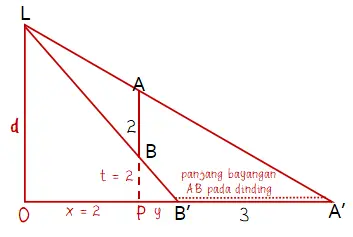
Dari kesebangunan segitiga LOB’ dan BPB’ dapat dibentuk persamaan (i):

Dari kesebangunan segitiga LOA’ dan APA’ dapat dibentuk persamaan (ii):

*kali silang
(y + 2)(y + 3) = 2y(y + 5)

Sehingga,

y² + 5y + 6 = 2y² + 10y

y² + 5y – 6 = 0

*faktorkan
(y + 6)(y – 1) = 0

Diperoleh dua nilai y yaitu y = –6 atau y = 1. Untuk jarak, nilai yang memenuhi adalah nilai y positif yaitu y = 1.  

Substitusi nilai y = 1 pada persamaan (i):

d = 2 × 3 = 6

Jadi,  jarak lampu ke dinding adalah 6 meter.

Soal 3

Diketahui t = 1 dan x = 4. Semula jarak lampu L ke dinding adalah 7 meter, kemudian lampu L bergerak sepanjang garis lurus sejauh 2√2 meter dengan mempertahankan posisi titik A’, jarak titik A’ dan B’ adalah … meter.
(A) 2
(B) 2¹/₄ 
(C) 2¹/₂ 
(D) 2³/₄ 
(E) 3

Jawab: (C)

Misalkan titik lampu yang baru adalah L’ maka jarak L ke L’ adalah 2√2 meter.

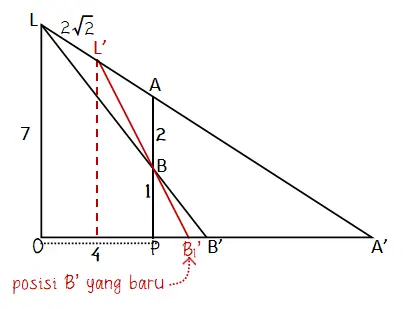
Dari kesbangunan segitiga APA’ dan LOA’ diperoleh

7PA’ = 3(PA’ + 4)

7PA’ = 3PA’ + 12

4PA’ = 12

Diperoleh panjang PA’ = 3 meter, sehingga panjang OA’ = 4 + 3 = 7 meter. Selanjutnya, panjang LA’ dicari menggunakan Teorema Pythagoras.

Panjang LA’ = √(LO² + OA’²)  

= √(7² + 7²)

= √(2×7²) = 7√2 meter

 Berikutnya panjang AA’ dapat dicari menggunakan Teorema Pythagoras dari segitiga APA’. Diperoleh nilai AA’ = 7√2 meter, sehingga AL = 7√2 – 3√2 = 4√2 meter.

Diketahui jarak LL’ =  4√2 meter, maka jarak AL’ = 4√2 – 2√2 = 2√2 meter. Ruas garis yang melalui lampu L’ membagi OP menjadi dua sama panjang 2 meter.

Dari segitiga APA’ dan L’QA’ dapat diperoleh jarak L’ ke dinding:

QL’ = 5 meter

Selanjutnya, dari kesebangunan segitiga QB₁’L’ dan segitiga PB₁’B dapat diperoleh persamaan berikut.

2 + PB₁’ = 5PB₁’

4PB₁’ = 2

PB₁’ = ²/₄ = ¹/₂ 

Sehingga jarak titik A’ dan B’ yang baru A’B1’ = PA’ – PB₁’ = 3 – 1/2 = 2¹/₂ meter.

Soal 4

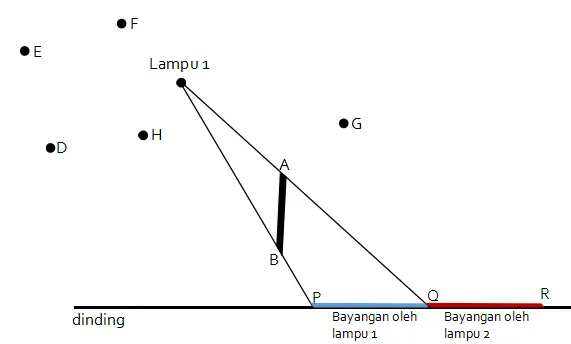
Untuk suatu keperluan tertentu, ditambahkan lampu kedua. Jika PQ adalah bayangan tembok oleh lampu 1 dan QR adalah bayangan tembok oleh lampu 2, posisi yang mungkin untuk lampu 2 adalah di titik ….
(A) D
(B) E
(C) F
(D) G
(E) H

Jawab: (B)

Untuk menentukan yang mungkin untuk lampu 2 dilakukan dengan menarik garis lurus dari titik R melalui titik A. Lampu yang dilewati sinar garis tersebut merupakan posisi yang paling mungkin untuk lampu 2.

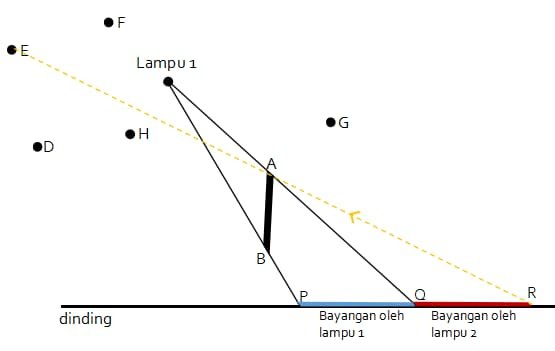
Jadi, posisi yang mungkin untuk lampu 2 adalah di E (B).