Pada proses regresi linear terdapat langkah mencari garis lurus. Garis lurus yang dicari adalah garis lurus yang paling tepat terhadap titik-titik yang ada pada diagram pencar. Salah satu cara untuk mencari persamaan garis lurus ini adalah metode kuadrat terkecil.
Penjelasan lebih lanjut mengenai mengenai metode kuadrat terkecil ada di bawah.
Daftar isi:
Rumus Jumlah Kuadrat (Sum of Square – SS)
Hasil akhir dari metode kuadrat terkecil pada regresi linear adalah persamaan garis lurus. Bentuk umum persamaan garis lurusnya adalah y = a + bx. Keterangan: y = nilai variabel dependen yang diprediksi, x = nilai variabel independent, a = titik potong sumbu y, b = gradien garis regresi.
Nilai a dan b pada persamaan garis regresi linear perlu dihitung menggunakan rumus jumlah kuadrat. Nilai b dihitung menggunakan rumus b = SSxy/SSxx. Setelah mendapat nilai b, nilai a dapat diketahui dengan metode substitusi.
Untuk mencari nilai b, perlu menghitung SSxy dan SSxx. SSxy adalah jumlah kuadrat (sum of square) selisih variabel independen (x) terhadap rata-ratanya dan variabel y terhadap rata-ratanya. SSxx adalah jumlah kuadrat selisih variabel indenpenden (x) terhadap rata-ratanya.
Rumus hitung SSxx dan SSxy ada di bawah.

Keterangan: x = variabel bebas, y = variabel terikat, dan n = banyak data
Bagaimana cara menggunakan rumus SSxy dan SSxx ada pada langkah penyelesaian contoh soal di bawah.
Contoh Soal
Tabel berikut ini berisi informasi dari 12 siswa SMA mengenai rata-rata waktu yang digunakan per hari dalam menggunakan media sosial (Facebook, Twitter, dan lain-lain) dan internet untuk bersosialisasi dan hiburan, dan nilai mereka.
| Waktu | Nilai |
| 4,4 | 81 |
| 6,2 | 55 |
| 4,2 | 78 |
| 1,6 | 92 |
| 4,7 | 68 |
| 5,4 | 55 |
| 1,3 | 90 |
| 2,1 | 82 |
| 6,1 | 67 |
| 3,3 | 72 |
| 4,4 | 68 |
| 3,5 | 84 |
Keterangan: satuan waktu = jam per hari
1. Gambarlah diagram pencar dari data di atas!
2. Apakah diagram pencarnya memberikan indikasi bahwa ada hubungan linear antara rata-rata waktu untuk media social dan internet dengan nilai?
3. Tentukan persamaan garis regresinya. Ikutilah tahapan berikut ini.
a) Hitunglah nilai rata-rata x dan y
b) Hitunglah nilai SSxy dan SSxx
c) Hitunglah nilai b, gradien garis regresi, menggunakan hasil dari a) dan b)
d) Hitunglah nilai a, titik potong sumbu y, menggunakan hasil dari a) dan c)
e) Tentukan persamaan garis regresinya dengan menggunakan hasil dari c) dan d)
4. Interpretasikan masing-masing arti nilai a dan b yang ditemukan pada nomor 3
5. Hitunglah prediksi nilai siswa yang menggunakan rata-rata waktu 3,8 jam per hari untuk media sosial dan internet menggunakan persamaan garis regresi yang ditemukan pada nomor 3.
6. Hitunglah prediksi nilai siswa yang menggunakan rata-rata waktu 16 jam per hari untuk media sosial dan internet menggunakan persamaan garis regresi yang ditemukan pada nomor 3. Berikan komentar mengenai hasil yang ditemukan.
Langkah Metode Kuadrat Terkecil
Langkah pertama yang perlu dilakukan adalah membuat diagram pencar. Penjelasan caaranya ada di halaman cara membuat diagram pencar.
1) Membuat diagram pencar
Bentuk diagram pencar dari data rata-rata waktu yang digunakan per hari dalam menggunakan media sosial ada di bawah.
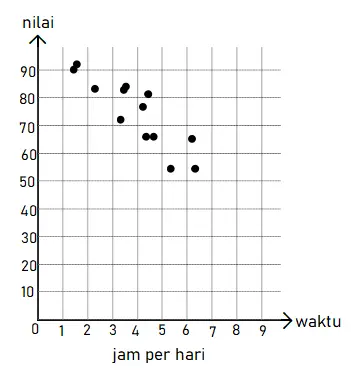
2) Interpretasi diagram
Dari gambar di atas, nampak bahwa titik-titik menyebar di sekitar garis lurus yang condong ke kiri.
Sehingga, jawaban pernyataan nomor 2 adalah terdapat indikasi hubungan linear antara rata-rata waktu untuk media sosial dan internet dengan nilai.
3) Menentukan persamaan garis regresi
Persamaan garis lurusnya di cari melalui beberapa langkah penyelesaian berikut.
| x | y | xy | x2 |
| 4,4 | 81 | 356,4 | 19,36 |
| 6,2 | 55 | 341 | 38,44 |
| 4,2 | 78 | 327,6 | 17,64 |
| 1,6 | 92 | 147,2 | 2,56 |
| 4,7 | 68 | 319,6 | 22,09 |
| 5,4 | 55 | 297 | 29,16 |
| 1,3 | 90 | 117 | 1,69 |
| 2,1 | 82 | 172,2 | 4,41 |
| 6,1 | 67 | 408,7 | 37,21 |
| 3,3 | 72 | 237,6 | 10,89 |
| 4,4 | 68 | 299,2 | 19,36 |
Jumlah x:
Ʃx = 4,4 + 6,2 + 4,2 + 1,6 + 4,7 + 5,4 + 1,3 + 2,1 + 6,1 + 3,3 + 4,4 + 3,5 = 47,2
Jumlah x2:
Ʃx2 = 19,36 + 38,44 + 17,64 + 2,56 + 22,09 + 29,16 + 1,69 + 4,41 + 37,21 + 10,89 + 19,36 = 215,06
Jumlah xy:
Ʃxy = 356,4 + 341 + 327,6 + 147,2 + 319,6 + 297 + 117 + 172,2 + 408,7 + 237,6 + 299,2 = 3.317,5
Sehingga,
SSxx = 215,06 – 185,653 = 29,407
SSxy = 3.317,5 – 3.508,533 = −191,033
Menentukan nilai b dan a:
Selanjutnya nilai SSxx = 29,407 dan SSxy = −191,033 digunakan untuk menghitung nilai b seperti berikut.
Nilai a dapat dicari dengan mengambil salah satu titik. Misalkan titik ketujuh yaitu (1,3; 90). Substitusi nilai b = –6,538; x = 1,3; dan y = 90 ke persamaan y = bx + a untuk mendapatkan nilai a.
90 = –6,538 × 1,3 + a
90 = –8,4994 + a
a = 90 + 8,4994
a = 98,4994
Persamaan garis regresi
Diperoleh nilai a = 98,4994 dan nilai b = –6,538. Jadi, persamaan regresi linear untuk data rata-rata waktu yang digunakan per hari dalam menggunakan media sosial adalah y = –6,538x + 98,4994.
4) Arti nilai a dan b
Arti nilai a = 98,4994
Saat nilai variabel bebas (variabel independen) sama dengan nol (x = 0), nilai variabel terikatnya atau variabel dependen sama dengan y = 98,4994. Dengan kata lain, saat tidak bermain sosial media, prediksi nilai siswa adalah 98,4994.
Arti nilai b = –6,538
Setiap kenaikan satu variabel independen membuat nilai variabel dependen berkurang 6,538. Setiap waktu bermain internet bertambah satu jam, prediksi nilai siswa akan turun 6,538.
5) Nilai prediksi 1
Jawaban nomor 5:
Saat rata-rata waktu 3,8 jam per hari untuk media sosial dan internet. Prediksi nilai siswa adalah y = –6,538x + 98,4994 = –6,538 × 3,8 + 98,4994 = –24.8444 + 98,4994 = 73,655.
6) Nilai prediksi 2
Jawaban nomor 6:
Saat rata-rata waktu 16 jam per hari untuk media sosial dan interne. Prediksi nilai yang akan diperoleh siswa adalah y = –6,538 × 16 + 98,4994 = –104.608 + 98,4994 = –6,1086.
Nilai siswa tidak mungkin negatif karena penilaian paling rendah adalah 0. Hasil jawaban nomor 6 merupakan ekstrapolasi. Yaitu hasil prediksi dari hubungan antar variabel yang berada di luar jangkauan data.
Sekian ulasan mengenai metode kuadrat terkecil pada proses regresi linear. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!