Operasi penjumlahan dan pengurangan vektor sedikit berbeda dengan operasi hitung bilangan pada umumnya. Secara geometris, penjumlahan dua buah vektor dapat dilakukan menggunakan aturan segitiga dan aturan jajargenjang. Sedangkan pada pengurangan vektor dilakukan melalui aturan penjumlahan vektor dengan membuat vektor pengurangan mempunyai arah vektor yang berkebalikan. Sehingga, penjumlahan dan pengurangan vektor memiliki bentuk rumus yang hampir sama.
Bentuk vektor biasnaya secara analitis dinyatakan dalam susunan urutan bilangan real yang diikuti oleh huruf yang menyatakan arah. Operasi penjumlahan dan pengurangan bilangan-bilangan yang menyatakan suatu besaran vektor dilakukan dengan penjumlahan/pengurangan bilangan dengan arah sama. Besaran vektor juga dapat dinyatakan secara geometris melalui ruas garis dengan sebuah arah anak panah.
Bagaimanakan cara melakukan penjumlahan dan pengurangan vektor? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Penjumlahan Vektor
- Pengurangan Vektor
- Sifat Penjumlahan dan Pengurangan Vektor
- Contoh Soal Penjumlahan dan Pengurangan Vektor (+Bahas)
Penjumlahan Vektor
Ada dua cara yang dapat dilakukan untuk menjumlahkan dua buah vektor. Kedua cara penjumlahan vektor meliputi aturan segitiga dan aturan jajar genjang.
Penjumlahan Vektor dengan Aturan Segitiga
Diketahui dua buah vektor a dan b dengan arah yang berbeda. Penjumlahan vektor dengan aturan segitiga dilakukan dengan menggabungkan ujung vektor a dengan pangkal vektor b. Vektor hasil penjumlahan vektor a dan vektor b sama dengan vektor yang menghubungkan pangkal vektor a ke ujung vektor b.
Gambaran penjumlahan vektor dan vektor b dengan aturan segitiga ditunjukkan seperti berikut.
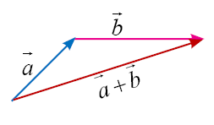
Jika besar sudut yang dibentuk oleh vektor a dan vektor b dapat dihitung dengan aturan cosinus.
Penjumlahan Vektor dengan Aturan Jajar Genjang
Penjumlahan vektor a dan b dengan aturan jajar genjang dilakukan dengan menggabungkan kedua ujung vektor. Hasil penjumlahan vektor dengan aturan jajar genjang adalah diagonal dari ujung kedua vektor dengan perpotongan proyeksi ujung kedua vektor. Gambaran penjumlahan vektor dengan aturan jajar genjang sesuai dengan kondisi berikut.
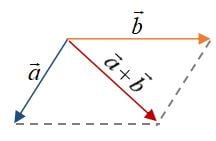
Diketahui dua vektor yaitu vektor a dan vektor b, esultan dari kedua vektor tersebut adalah vektor (a+b). Ketiga vektor pada penjumlahan vektor dengan aturan jajar genjang membentuk bangun jajargenjang. Dua buah ruas garis yang masing – masing sejajar dengan kedua vektor dan saling berpotongan akan membentuk bangun jajar genjang.
Rumus Penjumlahan Dua Vektor dan Panjangnya
Misalkan diketahui dua buah vektor pada dimensi 2 dinyatakan dalam vektor arah a = (x1, y1) dan vektor b = (x2, y2). Maka arah vektor untuk penjumlahan dua vektor dinyatakan dengan persamaan vektor arah (a + b) = (x1 + x2, y1 + y2).
Bagaimana dengan nilai panjang hasil penjumlahan kedua vektor?
Diketahui dua buah vektor:
a = xAi + yAj
b = xBi + yBj
Persamaan yang dapat digunakan untuk menentukan nilai penjumlahan kedua vektor sesuia dengan persamaan-persamaan berikut.

Baca Juga: Perbandingan Vektor
Pengurangan Vektor
Pengurangan dua buah vektor juga dapat dilakukan dengan metode segitiga dan jajar genjang. Cara pengurangan dua buah vektor dilakukan dengan membuat arah vektor menjadi berkebalikan. Perhatikan gambar pengurangan vektor di bawah untuk memahami bagaimana proses pengurangan vektor.
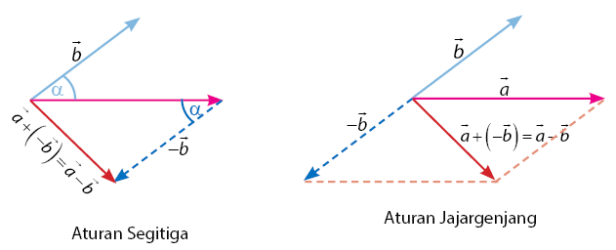
Rumus Pengurangan Dua Vektor dan Panjangnya
Diketahui dua buah vektor pada dimensi 2 dinyatakan dalam vektor arah a = (x1, y1) dan vektor b = (x2, y2). Maka arah vektor untuk penjumlahan dua vektor dinyatakan dengan persamaan vektor (a + b) = (x1 – x2, y1 – y2).
Bagaimana dengan nilai panjang hasil pengurangan dua buah vektor?
Diketahui dua buah vektor:
a = xAi + yAj
b = xBi + yBj
Persamaan yang dapat digunakan untuk menentukan nilai pengurangan kedua vektor untuk diberikan seperti berikut.

Baca Juga: Vektor Posisi dan Penyajian Vektor
Sifat Penjumlahan dan Pengurangan Vektor
Pada penjumlahan vektor memenuhi sifat komutatif dan asosiatif. Sedangkan pada pengurangan dua buah vektor tidak berlaku dua sifat tersebut. Berikut ini adalah sifat penjumlahan dan pengurangan vektor.

Baca Juga: Cara Menghitung Resultan Vektor 3 Arah
Contoh Soal Penjumlahan dan Pengurangan Vektor (+Bahas)
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan materi penjumlahan dan pengurangan vektor. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan cara penjumlahan dan pengurangan vektor. Sobat idschool dapat menggunakan pembahasan soal tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Penjumlahan dan Pengurangan Vektor
Diketahui 3 vektor yang dinyatakan dengan persamaan seperti di bawah.
a = 3i – 2j
b = –i + 4j
c = 7i – 8j
Jika vektor r dinyatakan dalam persamaan vektor r = k·a + m·b maka nilai k + m adalah ….
A. 3
B. 2
C. 1
D. -1
E. -2
Pembahasan:
Menentukan persamaan vektor:
r = k·a + m·b
7i – 8j = k(3i – 2j) + m(–i + 4j)
7i – 8j = 3ik – 2jk – im + 4jm
7i – 8j = 3ik – im – 2jk + 4jm
7i – 8j = (3k – m)i + (–2k + 4m)j
Berdasarkan persamaan di atas dapat diperoleh dua persamaan yaitu,
- 3k – m = 7
- 2k – 4j = 8
Selanjutnya, kita dapat menentukan nilai k dan m berdasarkan dua persamaan di atas.
Mencari nilai k:
Mencari nilai m:
Diperoleh nilai k = 2 dan m = –1, jadi nilai k + m = 2 + (–1) = 2 –1 = 1.
Jawaban: C
Contoh 2 – Soal Penjumlahan dan Pengurangan
Diketahui dua buah titik terletak di A (2,5) dan B (7,9). Vektor perpindahan dari titik A ke titik B adalah ….
A. 41
B. 25
C. 14
D. √41
E. √14
Pembahasan:
Diketahui:
A = 2i + 5j
B = 7i + 9j
Mencari vektor perpindahan (r):
r = B – A
= (7 – 2)i + (9 – 5)j
= 5 i + 4 j
Menghitung nilai r atau B – A:

Jadi, vektor perpindahan dari titik A ke titik B adalah .
Jawaban:
Demikianlah tadi ulasan materi penjumlahan dan pengurangan vektor serta sifat-sifatnya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Materi Vektor Matematika SMA

buatkan rangkuman tentang pembahasan selisih 2 vektor! untuk dipresentasikan
banyak typo nya.
Penjumlahan vektor antara metode jajar genjang dan metode segitiga memiliki arah dan besar resultan yang berbeda.