Vektor adalah besaran yang memiliki arah yang digambarkan oleh sebuah ruas garis dengan satu ujung anak panah pada salah satu sisinya. Vektor menyatakan posisi benda dalam titik-titik koordinat. Bahasan perbandingan vektor digunakan untuk mengetahui di mana letak suatu titik yang memiliki suatu perbandingan nilai.
Sebuah ruas garis yang memiliki titik pangkal dan ujung dapat dinyatakan dalam sebuah vektor. Jika diberikan sebuah titik A dan B dengan koordinatnya masing-masing maka terbentuk suatu ruas garis AB. Sebuah titik P berada pada ruas garis AB akan membentuk sebuah perbandingan panjang. Gambar vektor seperti deskripsi yang telah disebutkan tersebut diberikan seperti di bawah.
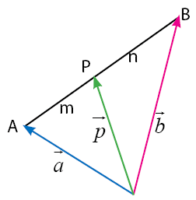
Titik P terletak pada ruas garis AB dapat diketahui posisinya melalui besar perbandingan ruas garis serta koordinat titik A dan B. Bagaimanakah cara mengetahui koordinat titik P? Sobat idschool dapat menggunakan rumus pada perbandingan vektor yang akan dibahas pada ulasan di bawah
Table of Contents
- Perbandingan Vektor di Dalam Ruas Garis
- Perbandingan Vektor di Luar Ruas Garis
- Contoh Soal dan Pembahasan
Perbandingan Vektor di Dalam Ruas Garis
Titik P membagi ruas garis AB dengan besar perbandingan m dan n. Kondisi ini terjadi saat titik P berada di antara titik A dan B. Cara menentukan koordinat P pada perbandingan vektor pada ruas garis dengan titik P berada di dalam dapat dilihat pada persamaan sebagai berikut.
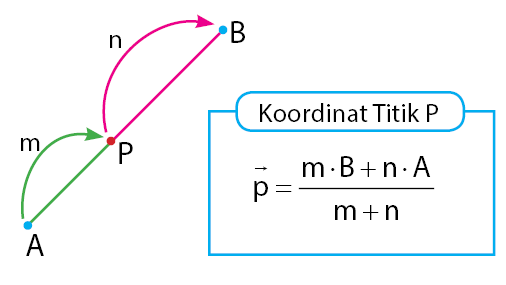
Baca Juga: Vektor Posisi, Penyajian Vektor, dan Panjang Vektor
Perbandingan Vektor di Luar Ruas Garis
Perbandingan Vektor di Luar pada Ruas Garis untuk kasus titik pembagi P berada di luar ruas garis dibedakan menjadi dua kondisi. Pertama adalah titik P yang membagi vektor pada ruas garis berada sebelum ruas garis. Kedua adalah titik P yang membagi vektor pada ruas garis berada setelah ruas garis. Perbedaan kondisi ini didasarkan pada besar nilai pembanding pertama dan kedua.
Titik pembagi P berada sebelum ruas garis AB
Kondisi pertama, terjadi saat titik P membagi ruas garis AB di luar dengan letak titik P berada sebelum ruas garis AB. Dengan kata lain, letak titik P berada sebelum titik A. Kondisi ini terjadi saat nilai pembanding pertama (m) lebih kecil dari pembanding ke dua (n). Sehingga memenuhi m < n. Berikut ini adalah persamaan yang dapat digunakan untuk menentukan letak koordinat titik P.
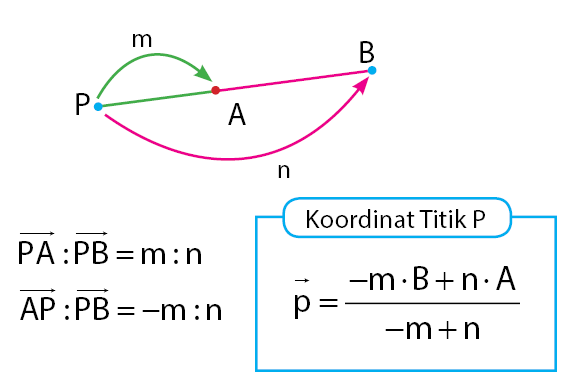
Baca Juga: Perkalian Skalar Vektor
Titik pembagi P berada setelah ruas garis AB
Kondisi kedua adalah sebuah titik P membagi ruas garis AB di luar dengan P terletak setelah ruas garis AB. Keadaan ini terjadi saat nilai pembagi pertama (m) lebih besar dari pembagi kedua (n). Atau kondisinya memenuhi m > n. Untuk menentukan koordinat P dapat menggunakan persamaan di bawah.
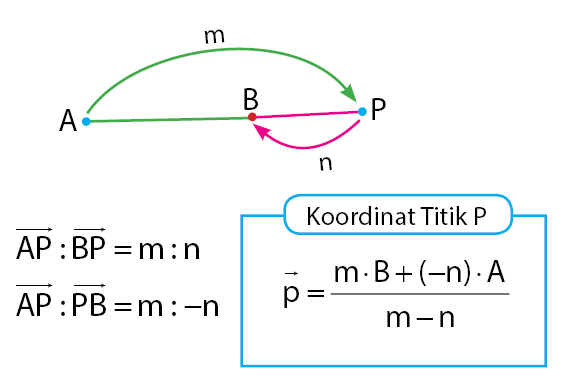
Baca Juga: Proyeksi Vektor (Skalar dan Ortogonal)
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh Soal 1: Perbandingan Vektor di Dalam dan Perbandingan Vektor di Luar
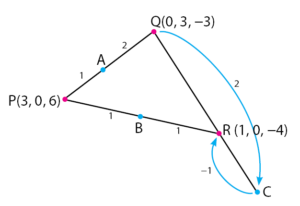
Titik sudut segitiga PQR adalah P(3, 0, 6), Q(0, –3, –3), dan R(1, 0, –4). Titik A membagi PQ di dalam dengan perbandingan 1 : 2. Titik B merupakan titik yang berada di tengah – tengah ruas garis PR. Sedangkan titik C membagi QR di luar dengan perbandingan 2 : 1.
Nilai perbandingan panjang AB : BC adalah ….
A. 1 : 3
B. 3 : 1
C. 1 : 2
D. 2 : 1
E. 2 : 3
Pembahasan:
Ilustrasi segitiga pada soal dapat dilihat pada gambar di bawah.
Mencari titik koordinat A:
A = 2(3, 0, 6) + (0, 3, -3)/2 + 1
A = (6, 0, 12) + (0, 3, -3)/3
A = (6 + 0, 0 + 3, 12 + (-3))/3
A = (6, 3, 9)/3
A = (2, 1, 3)
Mencari titik koordinat B:
B = (3, 0, 6) + (1, 0, -4)/1 + 1
B = (3 + 1, 0 + 0, 6 + (-4))/2
B = (4, 0, 2)/2
B = (2, 0, 1)
Mencari titik koordinat C:
C = 2(1, 0, -4) + (-1)(0, 3, -3)/2 – 1
C = (2, 0, -8) + (0, -3, 3)/1
C = (2 + 0, 0 – 3, -8 + 3)/1
C = (2, -3, -5)/1
C = (2, -3, -5)
Menghitung panjang AB:
AB = B ‒ A
AB = (2, 0, 1) ‒ (2, 1, 3)
AB = ( 2 ‒ 2, 0 ‒ 1, 1 ‒ 3)
AB = (0, ‒1, ‒2)
| AB |2 = 02 +(‒1)2 + (‒2)2
| AB |2 = 0 + 1 + 4 = 5
| AB | = √5
Menghitung panjang BC:
BC = C ‒ B
BC = (2, ‒3, ‒5) ‒ (2, 0, 1)
BC = ( 2 ‒ 2, ‒3 ‒ 0, ‒5 ‒ 1)
CB = (0, ‒3, ‒6)
| BC |2 = 02 +(‒3)2 + (‒6)2
| BC |2 = 0 + 9 + 36 = 5
| BC | = √45 = √(9×5) = 3√5
Mencari perbandingan AB : BC,
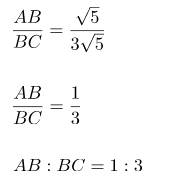
Jawaban: A
Baca Juga: Peluang Kejadian Majemuk dan Bersyarat
Contoh Soal 2: Perbandingan Vektor pada Ruas Garis
Diketahui P(3, 1, 4) dan Q(6, –5, 1). Absis titik T yang membagi PQ di dalam dengan perbandingan 2 : 1 adalah ….
A. – 5
B. – 3
C. – 2
D. 2
E. 5
Pembahasan:
Perhatikan gambar di bawah!

Mencari koordinat titik T:
T = 2(6, -5, 1) + 1(3, 1, 4)/2 + 1
T = (12, -10, 2) + (3, 1, 4)/3
T = (15, -9, 6)/3
T = (5, -3, 2)
Jadi nilai absis (titik x) dari titik T adalah 5.
Jawaban: E
Demikianlah pembahasan perbandingan vektor pada ruas garis yang terdiri dari perbandingan di dalam dan perbandingan di luar.
Vektor dapat menunjukkan posisi benda secara baik. Fungsi ini dimanfaatkan pada dunia penerbangan. Sebuah pesawat terbang yang mengudara dapat terbang dan sampai tujuan karena dipandu melalui radar. Letak posisi pesawat di udara dapat dinyatakan secara pasti melalui koordinat.
Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Materi Vektor Matematika SMA

Mencari koordinat titik A nya, sepertinya kurang tepat karena menggunakan rumus m.A+ n.B / m+n sedangkan seharusnya m.B + n.A /m+n
Diatas itu pake rumus n.A+m.B/m+n, jadi sebenarnya sama aja karena rumusnya itu dijumlah, ga akan mempengaruhi hasil walaupun dibalik (n.A+m.B = m.B+n.A)
Halo Kana, untuk rumus titik A di tengah vektor PQ dengan perbandingan 1 : 2 dapat menggunakan rumus: A = 2P + Q/(2+1) rumus tersebut diperoleh dari penjabaran berikut.
PA : AQ = 1 : 2
PA x 2 = 1 x AQ
(A – P) x 2 = 1 x (Q – A)
2A – 2P = Q – A
2A + A = 2P + Q
3A = 2P + Q
A = (2P + Q)/3
Terimakasih sudah mengunjungi idschool, salam sukses selalu!