Rumus trigonometri cos (A+B) memiliki bentuk identitas cos(A + B) = cos A ∙ cos B − sin A ∙ sin B. Bentuk identitas trigonometri tersebut dapat dibuktikan dengan beberapa cara. Salah satu cara yang digunakan dalam pembuktian rumus trigonometri cos (a+b) adalah menggunakan kesamaan jarak.
Bentuk identitas cos(A + B) = cos A ∙ cos B − sin A ∙ sin B selanjutnya dapat digunakan dalam pembuktian rumus trigonometri cos(A − B) = cos A ∙ cos B + sin A ∙ sin B. Bagaimana cara pembuktian rumus trigonometri cos (A+B) dan cos (A-B)? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Cara Pembuktian Rumus Trigonometri Cos (A+B)
Misalkan sebuah titik P berada pada sumbu x. Koordinat titik P pada awalnya adalah (1, 0). Titik P kemudian sebanyak dua kali dengan besar sudut A dan B.
Perpindahan titik P nampak seperti gambar berikut.

Koordinat titik P setelah diputar sebesar sudut A adalah P'(cos A, sin A). Untuk koordinat titik P setelah diputar sebesar sudut B adalah P”(cos B, sin B).
Sebuah titik M mengalami transformasi geometri dengan besar sudut putar B dan sudut pusat O dari titik A. Titik N mengalami transformasi dengan besar sudut putar −B dan sudut pusat O dari titik P.
Sehingga diketahui koordinat untuk titik M (cos (A+B), sin (A+B)). Sementara koordinat titik N(cos B, −sin B), ingat cos (−B) = cos B dan sin (−B) = −sin B. Bagaimana letak posisi titik M dan N terdapat seperti gambar berikut.
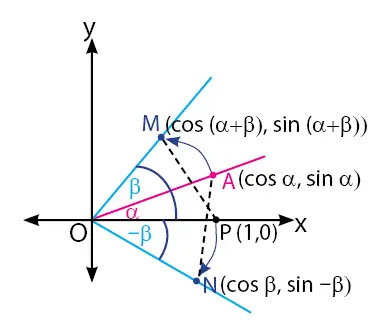
Jarak titik P (1, 0) ke titik M adalah |PM| yang dapat dihitung dengan rumus jarak antara dua titik. Persamaan untuk panjang |PM| dapat dibentuk dengan cara berikut.
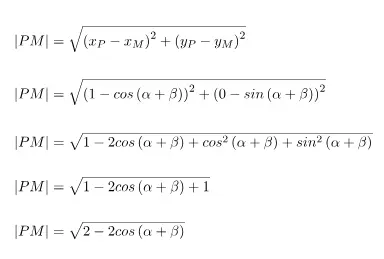
Jarak titik A ke titik N dapat dihitung dengan rumus jarak antara dua titik. Persamaan untuk panjang |AN| dapat dibentuk dengan cara berikut.
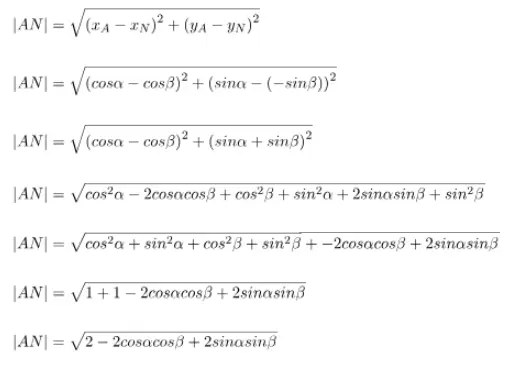
Secara geometri, panjang PM sama dengan AN sehingga dapat dibentuk persamaan |PM| = |AN|. Dengan menyederhanan persamaan tersebut selanjutnya akan diperoleh identitas rumus cos (A + B) seperti yang terdapat pada langkah penyelesaian berikut.

Diperoleh hasil akhir: cos (A+B) = cos A ∙ cos B – sin A ∙ sin B (Terbukti)
Baca Juga: Turunan Fungsi Trigonometri
Contoh Penggunaan Rumus Cos (A+B)
Soal:
Tentukan nilai cos 75o!
Jawab:
Besar sudut 75o bukan merupakan sudut istimewa. Namun besar sudut tersebut dapat dibentuk dari penjumlahan dua sudut istimewa yaitu 45o dan 30o.
Rumus trigonometri cos (A+B):

Diketahui:
cos 45o = sin 45o = 1/2√2
cos 30o = 1/2√3
sin 30o = 1/2
Cara menentukan nilai dari cos 75o terdapat pada langkah penyelesaian berikut.

Jadi, nilai dari cos 75o = 1/4(√6 − √2)
Cara Pembuktian Rumus Trigonometri Cos (A-B)
Bentuk identitas cos (A+B) = cos A cos B − sin A sin B di atas dapat digunakan untuk pembuktian rumus cos (A−B). Caranya adalah dengan mengubah sudut B menjadi sudut −B.
Pembuktian rumus trigonometri cos (A−B) = cos A cos B + sin A sin B terdapat pada operasi di bawah.
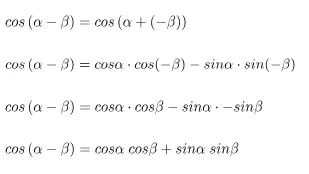
Diperoleh hasil akhir: cos (A−B) = cos A cos B + sin A sin B (terbukti)
Contoh Penggunaan Rumus Cosi (A-B)
Soal:
Tentukan nilai cos 105o!
Jawab:
Besar sudut 105o bukan merupakan sudut istimewa, tetapi merupakan selisih dua sudut istimewa yaitu 135o dan 30o.
Diketahui:
cos 135o = −1/2√2
sin 135o = 1/2√2
cos 30o = 1/2√3
sin 30o = 1/2
Rumus yang digunakan:

Gunakan rumus identitas trigoometri di atas untuk menenutkan nilai cos 105o seperti penyelesaian berikut.
Menghitung nilai cos 105o:
cos 105o = cos (135o − 30o)
= cos 135o ∙ cos 30o + sin 135o ∙ sin 30o
= (−1/2√2)(1/2√3) + 1/2√2(1/2)
= −1/4√6 + 1/4√2
= 1/4(√2 − √6)
Jadi, nilai dari cos 105o = 1/4(√2 − √6).
Demikianlah tadi ulasan bagaimana pembuktian rumus trigonometri cos (A+B) dan cos (A-B). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!