Rumus simpangan rata-rata, ragam, dan simpangan termasuk dalam bahasan statistika yang menunjukkan bagaiman karakteristik dari sekelompok data. Simpangan rata-rata menyatakan penyebaran nilai dari nilai rata-rata pada sekelompok data. Ragam atau variansi menyatakan perbandingan antara simpangan baku/standar deviasi dengan nilai rata-ratanya, dala bentuk persen. Simpangan baku adalah ukuran sebaran statistik, nilai yang menggambarkan rata-rata jarak penyimpangan titik-titik data yang diukur dari nilai rata-rata data tersebut.
Nilai dari simpangan rata-rata digunakan untuk memberikan representatif data yang tepat, apakah data dapat menjadi wakil atau tidak. Ragam atau varians (variance) digunakan untuk tingkat penyebaran dari kumpulan data, semakin menyebar data maka semakin besar kaitan ragam dengan rata-rata. Nilai dari simpangan baku digunakan untuk membandingkan suatu kumpulan data dengan kumpulan data yang lain.
Bagaimana bentuk rumus simpangan rata-rata, ragam/variansi, dan simpangan baku? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
- Rumus Simpangan Rata-Rata, Ragam, dan Variansi pada Data Tunggal
- Rumus Simpangan Rata-Rata, Ragam, dan Variansi pada Data Kelompok
- Contoh Soal dan Pembahasan
Rumus Simpangan Rata-Rata, Ragam, dan Variansi pada Data Tunggal
Data tunggal adalah sekelompok data yang penyajiannya diberikan dengan menampilkan semua data satu-persatu. Rumus simpangan rata-rata, rumus ragaml, dan rumus simpangan baku untuk data tunggal sesuai dengan persaman-persamaan berikut.
1) Simpangan Rata-Rata (SR)
Untuk xi adalah nilai datum ke-i, x̄ adalah rata-rata, dan n adalah jumlah frekuensi dari semua data. Rumus simpangan rata-rata data tunggal sesuai dengan persamaan berikut.

2) Variansi/Ragam (S2)
Variansi menyatakan rata-rata dari kuadrat dari selisih data ke-i dengan rata-rata data. Untuk xi adalah nilai datum ke-i, x̄ adalah rata-rata, dan n adalah jumlah frekuensi semua data. Rumus variansi data tunggal dapat dihitung menggunakan rumus berikut.

3) Standar Deviasi (Simpangan Baku)
Standar deviasi (stdv) atau simpangan baku adalah akar dari ragam. Untuk xi adalah nilai datum ke-i, x̄ adalah rata-rata, dan n adalah jumlah frekuensi semua data. Rumus standar deviase untuk data tunggal dapat dihitung menggunakan rumus berikut.

Baca Juga: Rumus Kuartil, Desil, dan Persentil
Rumus Simpangan Rata-Rata, Ragam, dan Variansi pada Data Kelompok
Data kelompok adalah sekumpulan data yang disajikan dalam bentuk kelas-kelas. Rumus simpangan rata-rata, rumus ragam/variansni, dan rumus simpangan baku untuk data kelompok sesuai dengan persamaan-persamaan berikut.
1)Simpangan Rata-rata (SR)
Untuk fi adalah frekuensi kelas ke-i, xi adalah nilai tengah kelas ke-i, x̄ adalah rata-rata data kelompok, k adalah panjang interval kelas, dan n adalah jumlah frekuensi semua data. Rumus simpangan rata-rata untuk data kelompok menggunakan persamaan berikut.

2) Variansi/Ragam
Pengertian ragam pada data kelompok sama dengan ragam data tunggal. Hanya rumus yang digunakan sedikit berbeda.
Untuk fi adalah frekuensi kelas ke-i, xi adalah nilai tengah kelas ke-i , x̄ adalah rata-rata, dan k adalah panjang interval kelas, dan n adalah jumlah frekuensi dari semu kelas. Rumus ragam untuk data kelompok dapat menggunakan persamaan di bawah.

3) Standar Deviasi (Simpangan Baku)
Stnadar deviasi atau simpangan baku untuk data kelompok merupakan akar dari variansi dari data kelompok. Untuk fi adalah frekuensi kelas ke-i, xi adalah nilai tengah kelas ke-i , x̄ adalah rata-rata, dan k adalah panjang interval kelas, dan n adalah jumlah frekuensi dari semu kelas.
Rumus standar deviasi untuk data kelompok dapat menggunakan persamaan di bawah.

Baca Juga: Jangkauan, Hamparan, dan Kuartil
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara menggunakan rumus simpangan rata-rata, ragam/variansi, satau simpangan baku.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Penggunaan Rumus Simpangan Rata-Rata
Diketahui data terurut (3x – 3), 2x, (2x + 1), (3x – 1), (3x + 3), dan (4x + 1). Diketahui bahwa jangkauan data adalah 6, simpangan rata-rata data tersebut adalah ….
A. 1
B. 2
C. 3
D. 4
E. 5
Pembahasan:
Dari soal dapat diketahui data terurut (3x – 3), 2x, (3x – 1), (2x + 2), (3x + 3), (4x + 1)
Diperoleh
Nilai minimum: xmin = 3x – 3
Nilai maksimum: xmax = 4x + 1
Mencari nilai x:
Jangkauan = xmax – xmin
6 = 4x + 1 – (3x – 3)
6 = 4x + 1 – 3x + 3 = x + 4
x = 6 – 4 = 2
Substitusi nilai x = 2 ke setiap persamaan data untuk mendapatkan nilai-nilainya seperti berikut.
| data ke- | nilai |
| 1 | 3x – 3 = 3(2) – 3 = 6 – 3 = 2 |
| 2 | 2x = 2 x 2 = 4 |
| 3 | 3x – 1 = 3(2) – 1 = 6 – 1 = 5 |
| 4 | 2x + 2 = 2(2) + 2 = 4 + 2 = 6 |
| 5 | 3x + 3 = 3(2) + 3 = 6 + 3 = 9 |
| 6 | 4x + 1 = 4(2) + 1 = 8 + 1 = 9 |
Enam data terurut menjadi: 3, 4, 5, 6, 9, 9
Mencari rata-rata (x̄):
x̄ = (3+4+5+6+9+9) : 6
x̄ = 36 : 6 = 6
Mencari simpangan Rata-rata (SR):

Jadi, simpangan rata-rata data tersebut adalah 2.
Jawaban: B
Contoh 2 – Soal Mencari Ragam/Variansi
Perhatikan penyajian berat badan (dalam kg) sekelompok siswa disajikan dalam histogram berikut.

Ragamnya adalah ….
A. 30 kg
B. 35 kg
C. 40 kg
D. 45 kg
E. 50 kg
Pembahasan:
Dari data yang diberikan pada soal dapat diketahui bahwa penyajian data diberikan dalam bentuk data kelompok. Rata-rata data kelompok pada histogram dapat dicari seperti pada cara berikut.
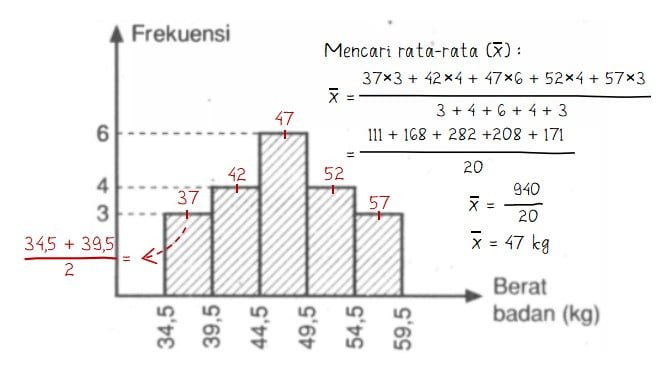
Mencari nilai ragam (S2):

Jadi, ragamnya adalah 40 kg
Jawaban: C
Sekian pembahasan mengenai rumus simpangan rata-rata, ragam, dan simpangan baku. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Rumus Mean,Median, dan Modus Data Kelompok

Untuk contoh soal yg simpangan rata” 7 dapat darimana ya? Soalnya dari awal harusnya fi nya 6
Kayanya Salah ketik deh
Tolong bantu saya mengerjakan tugas saya mengenai simpangan baku dan ragam
Mana sini ku bantu