ΔABC siku-siku di B. Titik D terletak pada sisi AC sehingga ΔBDC siku-siku di D, ∠ABD = 30o, BD = 3, dan ABDE merupakan jajar genjang.
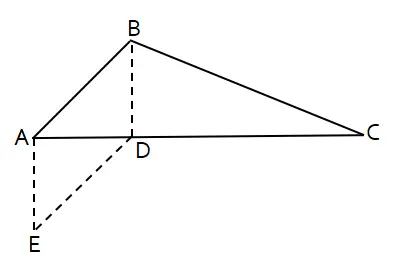
Pertanyaan:
Soal 1
Besar ∠BAE adalah ….
(A) 150o
(B) 135o
(C) 130o
(D) 120o
(E) 110o
Jawab: (A)
Dari keterangan yang diberikan pada soal dapat diperoleh ukuran-ukuran berikut.
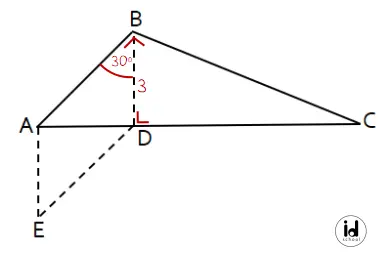
Besar ∠BAE sama dengan jumlah besar ∠BAD dan ∠DAE. Perhatikan segitiga ABD! Diketahui besar ∠ABD = 30o dan besar ∠ADB = 90o (siku-siku). Jumlah ketiga sudut dalam segitiga selalu sama dengan 180o.
1) Menghitung besar ∠BAD:
m ∠BAD = 180o – (30o + 90o)
m ∠BAD = 180o – 120o = 60o
Selanjutnya perhatikan jajar genjang ABDE, diketahui bahwa garis AE sejajar dengan garis BD. Besar ∠DAE sama dengan besar pelurus ∠BDC karena keduanya merupakan pasangan sudut sehadap. Besar pelurus sudut BDC = 180o – 90o = 90o sehingga besar ∠DAE = 90o.
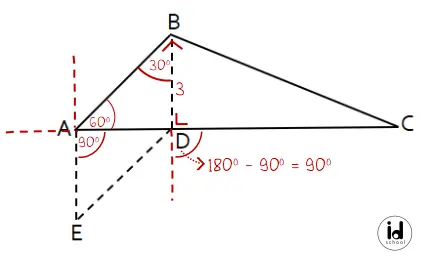
Sehingga,
m∠BAE = m∠BAD + m∠DAE
m∠BAE = 60o + 90o = 150o
Jadi, besar BAE adalah 150o.
Soal 2
AC = ….
(A) 4
(B) 4√2
(C) 4√3
(D) 5√3
Jawab: (C)
Perhatikan segitiga ABC!
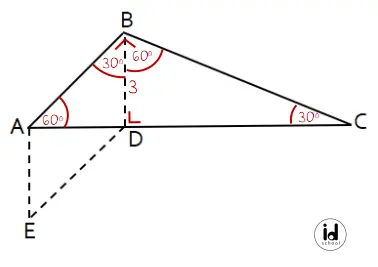
Panjang AB dan BC perlu dihitung terlebih dahulu untuk bisa menghitung panjang AC. Panjang garis AB dan BC dapat dihitung menggunakan rumus pada Aturan Sinus.
1) Menghitung panjang AB:
2) Menghitung panjang BC:
1/2BC = 3
BC = 3×2 = 6
3) Menghitung panjang AC:
AC = √(AB2 + BC2)
AC = √[(2√3)2 + 62]
AC = √(12 + 36) = √48
AC = √(16×3) = 4√3
Jadi, panjang AC = 4√3
Soal 3
Luas jajaran genjang ABDEE adalah ….
(A) 9
(B) 4√3
(C) 6
(D) 3√3
Jawab: (D)
Rumus luas jajar genjang: Luas = alas × tinggi
Ukuran panjang sisi-sisi ABDE terdapat pada gambar berikut.

Dari keterangan pada gambar dapat diketahui panjang alas jajaran genjang adalah ED = AB = 2√3. Sementara untuk tinggi jajaran genjang perlu dihitung terlebih dahulu.
Panjang tinggi jajaran genjang t dapat dihitung dengan rumus fungsi trigonometri untuk fungsi sinus seperti berikut.
Diketahui panjang alas jajaran genjang ABDE adalah ED = 2√3 dan tinggi jajaran genjang t = 3/2. Sehingga luas jajaran genjang dapat dihitung dengan cara berikut.
Menghitung luas jajaran genjang:
Luas = alas × t = ED × t
Luas = 2√3 × 3/2 = 3√3
Jadi, luas jajaran genjang ABDEE adalah (D) 3√3.