Jumlah 25 suku pertama deret tersebut adalah ….

Diketahui suku ke-3 dan suku ke-7 suatu barisan aritmetika berturut-turut adalah 28 dan 44. Jumlah 25 suku pertama deret tersebut adalah ….
A. 1.600
B. 1.650
C. 1.700
D. 1.800
E. 1.850

Jawab: C

Berdasarkan keterangan pada soal diketahui nilai U₃ = 28 dan U₇ = 44. Dari dua nilai suku ke-n barisan aritmatika tersebut dapat dibentuk dua persamaan dengan variabel a (suku pertama) dan b (beda) seperti berikut.

• U₃ = 28 → a + 2b = 28
• U₇ = 44 → a + 6b = 44

Nila a dan b dari persamaan (i) a + 2b = 28 dan (ii) a + 6b = 44 dapat diselesaikan dengan metode substitusi/eliminasi pada SPLDV.

Mencari nilai beda (b):
Eliminasi a dari persamaan (i) dan (ii) untuk mendapatkan nilai b dengan cara berikut.

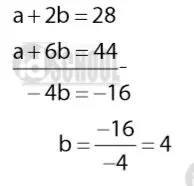
Diperoleh nilai b = 4 yang dapat digunakan untuk mencari nilai a (suku pertama) barisan aritmatika tersebut.

Mencari nilai suku pertama (a):
Substitusi nilai b = 4 ke persamaan (i) untuk mendapat nilai a.

a + 2b = 28
a + 2 × 4 = 28
a + 8 = 28
a = 28 – 8 = 20

Mencari jumlah 25 suku pertama:

Jadi, jumlah 25 suku pertama deret tersebut adalah 1.700