Nilai dari sin 2A adalah ….

Diketahui nilai cos A = −⁴/₅ dan sudut A berada di kuadran 2. Nilai dari sin 2A adalah ….
A. −⁶/₅
B. −¹³/₂₅
B. −²⁴/₂₅
D. ⁶/₅
E. ²⁴/₂₅

Jawab: C

Fungsi trigonometri terdiri dari fungsi sinus (sin), cosinus (cos), tangen (tan), serta kebalikan tiga fungsi tersebut yaitu fungsi cosec = ¹/_{sin x}, sec = ¹/_{cos x}, dan cotan = ¹/_{tan x}.

Funsi cosinus merupakan perbandingan antara sisi samping (x) dan miring (r). Sementara fungsi sinus adalah perbandingan sisi depan (y) dan sisi miring (r).

Dari soal diketahui,

• cos A = −⁴/₅
• Sudut A berada di kuadran 2, artinya fungsi trigonometri yang nilainya positif hanya fungsi sinus dan cosecan.

Dari nilai cos A = −⁴/₅ dapat diketahui nilai x = 4 dan r = 5. Di sini tanda negatif bisa dihiraukan. Tanda negatif tersebut menunjukkan bahwa fungsi cosinus di kuadran II adalah negatif.

Untuk mendapatkan nilai sinus membutuhkan nilai sisi depan (y) yang dapat dicari dengan Teorema Pythagoras seperti berikut.

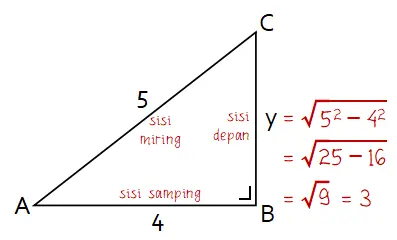
Membentuk fungsi sin A:

Cara menentukan nilai dari sin 2A adalah dapat menggunakan rumus identitas trigonometri sudut rangkap yaitu sin 2A = 2 ∙ sin A ∙ cos A. Substitusi nilai sin A = ³/₅ dan cos A = −⁴/₅ pada rumus identitas tersebut untuk menentukan nilai dari sin 2A.

Menentukan nilai sin 2A:
sin 2A = 2 ∙ sin A ∙ cos A
sin 2A = 2 ∙ (³/₅) ∙ (−⁴/₅)
sin 2A = −²⁴/₂₅

Jadi, nilai dari sin 2A adalah −²⁴/₂₅.