UTBK 2019/PK
Perhatikan gambar di bawah ini!

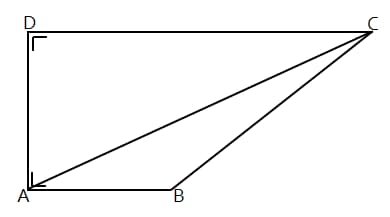
Pada trapesium siku-siku ABCD, AC = 9, jika luas ΔABC = 10, berapakah panjang DC?

• Pernyataan:
  • (1) AB = 4
  • (2) BC = 7

(A) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.

(B) Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.

(C) DUA Pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.

(D) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, dan pernyataan (2) SAJA cukup.

(E) Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab.

Jawab: (D)

• Dari soal diketahui:
  • AC = 9
  • Luas ΔABC = 10

Untuk pernyataan (1) AB = 4:

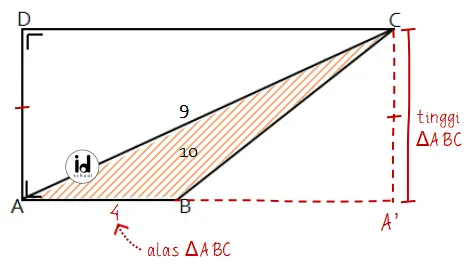
Dengan rumus luas segitiga dapat dibentuk persamaan untuk mengetahui panjang garis AD seperti berikut.

Menghitung panjang AD:

luas ΔABC = 10

2 × AD = 20

AD = 10 : 2 = 5

Selanjutnya, perhatikan segitiga ADC! Diketahui panjang AD = 5 dan AC = 9 sehingga panjang CD dapat dihitung menggunakan Teorema Pythagoras. Jadi, pernyataan (1) saja cukup untuk menjawab pertanyaan.

Untuk pernyataan (2) BC = 7:

Diketahui segitiga ABC dengan panjang sisi AC = 9, BC = 7, dan luas segitiga = 10.

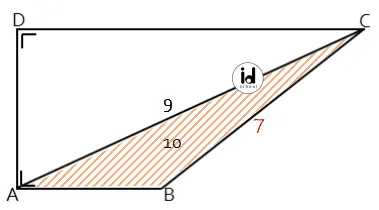
Segitiga ABC merupakan segitiga sembarang. Rumus luas segitiga sembarang adalah Luas = ¹/₂ × AC × BC × Sin C.

Sehingga,

10 = ¹/₂ × 9 × 7 × Sin C

20 = 63 × Sin C

Diketahui nilai Sin C = ²⁰/₆₃ sehingga nilai Cos C dapat diketahui. Selanjutnya, nilai Cos C dapat digunakan untuk menghitung panjang ruas garis AB menggunakan aturan cosinus. Ketika bisa mendapatkan AB, panjang ruas garis AB dapat diketahui.

Panjang AB kemudian dapat digunakan untuk mendapatkan panjang garis AD. Setelah mendapatkan panjang AD kemudian dapat digunakan untuk menghitung panjang DC dengan Teorema Pythagoras. Jadi, pernyataan (2) saja cukup untuk menjawab pertanyaan.

Kesimpulan: Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, dan pernyataan (2) SAJA cukup.