UTBK 2023/PM
Perhatikan gambar!

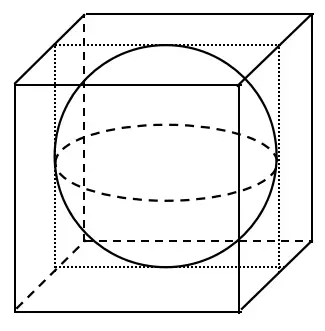
Sebuah bola berada dalam sebuah kubus yang memiliki diagonal sisi 6 cm.

Soal 1

Jika bola menyinggung semua sisi kubus seperti pada gambar maka volume bola adalah … cm³.

(A) 9√2π

(B) 16√2π

(C) 18√2π

(D) 25√2π

(E) 36√2π

Jawab: (A)

Diketaui panjang diagonal sisi 6 cm sehingga memenuhi persamaan s√2 = 6 (s = panjang rusuk kubus). Dengan demikian secara cepat dapat diketahui bahwa panjang rusuk kubus adalah s = ⁶/_√2 = 3√2 cm. Bola menyinggung semua sisi kubus, sehingga jari-jari bola adalah r = ¹/₂s = ¹/₂×3√2 = ³/₂√2 cm.

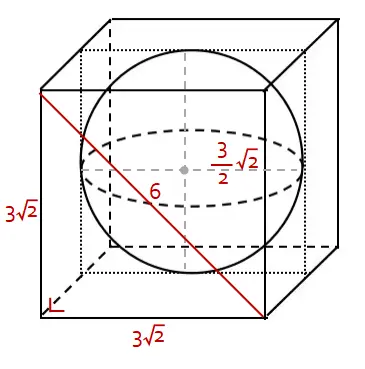
Menghitung volume bola:

Jadi, volume bola adalah V_bola = 9√2π cm³.

Soal 2

Jika bola menyinggung semua sisi seperti pada gambar, maka volume kubus di luar bola adalah …. cm³.

(A) 9π(6 − √2)

(B) 9π(√2 − 6)

(C) 9√2(6 − π)

(D) 9√2(π − 9)

(E) 6√2(9 − π)

Jawab: (C)

Volume kubus di luar bola sama dengan selisih antara volume kubus dengan volume bola. Dari perhitungan pada pembahasan soal nomor 1 diperoleh hasil volume bola adalah V_bola = 9√2π cm³. Sementara volume kubus belum diketahui sehingga perlu dihitung terlebih dahulu.

Menghitung volume kubus:

V_kubus = s³ = s×s×s

V_kubus = 3√2 × 3√2 × 3√2 = 54√2

Menghitung volume kubus di luar bola:

Volume = V_kubus − V_bola

Volume = 54√2 − 9√2π

Volume = 9√2(6 − π) cm³

Jadi, volume kubus di luar bola adalah 9√2(6 − π) cm³.