Jarak Titik ke Titik pada Dimensi Tiga (R3)

Jarak titik ke titik sama dengan panjang ruas garis terpendek yang menghubungkan kedua titik tersebut. Rumus jarak titik ke titik yang diketahui letak koordinatnya adalah d² = Δx² + Δy² atau d = √(Δx² + Δy²) . Misalnya, jarak antara titik A(3, 0) dan B(0, 4) sama dengan d = √(3² + 4²) = √25 = 5 satuan.

Dua titik yang terletak pada dimensi tiga dihitung dengan rumus jarak d² = Δx² + Δy² + Δz² atau d = √(Δx² + Δy² + Δz²). Misalnya untuk dua titik P(0, 7, 6) dan Q(5, 2, 1), jarak kedua titik tersebut adalah d = √(5² + 5² + 5²) = √125 = 5√3 satuan.

Rumus d hanya dapat digunakan untuk menghitung jarak kedua titik saat kedua letak titik koordinat diketahui. Misalnya pada sebuah kubus yang hanya diketahui panjang rusuknya.

Untuk jarak titik ke titik pada kubus atau titik pada bidang ruang lainnya sama dengan panjang suatu segmen garis. Cara menghitung panjang ruas garis dapat menggunakan Teorema Pythagoras, fungsi triggonometri, atau rumus lain yang berkaitan. Bagaimana cara menghitung jarak titik ke titik pada dimensi tiga? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

1) Jarak Titik ke Titik pada Kubus

Sebuah kubus memiliki 8 titik sudut, 6 bidang, dan 12 rusuk. Ruas garis yang menghubungkan dua titik sudut dengan jarak yang sama merupakan rusuk kubus.

Pada kubus terdapat garis diagonal bidang dan garis diagonal ruang. Garis diagonal bidang adalah ruas garis yang menghubungkan dua titik pada sebuah bidang secara diagonal. Garis diagonal ruang adalah ruas garis yang menghubungkan dua titik pada dua bidang yang berbeda secara diagonal.

Panjang diagonal bidang dan ruang pada kubus dapat dihitung dengan Teoremua Pythagoras. Untuk menyingkat waktu perhitungan, panjang diagonal bidang dan ruang pada kubus dapat menggunakan rumus cepat.

Panjang diagonal bidang pada kubus sama dengan rusuk√2, sedangkan panjang diagonal ruang pada kubus sama dengan rusuk√3. Untuk sebuah kubus yang memiliki panjang rusuk p satuan, panjang garis diagonal bidang = p√2 dan panjang garis diagonal ruang = p√3.

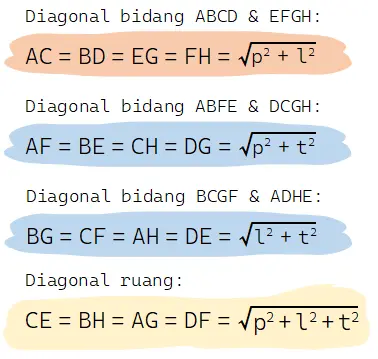
Selain rumus cepat jarak titik ke titik pada kubus untuk ruas garis diagonal bidang dan diagonal ruang, terdapat juga rumus cepat jarak dua titik lainnya. Beberapa rumus cepat jarak antara titik ke titik pada kubus dengan panjang rusuk a terdapat pada gambar berikut.

Baca Juga: Jarak Bidang ke Bidang pada Dimensi Tiga

2) Jarak Titik ke Titik pada Balok

Balok memiliki komponen penyusun yang sama seperti kubus yaitu 8 titik sudut, 6 bidang, dan 12 rusuk. Bedanya terdapat bentuk bidang, di mana bidang penyusun balok berbeda dengan bidang yang menyusun kubus.

Pada balok, ada tiga garis diagonal bidang dengan panjang yang berbeda. Panjang garis diagonal bidang pada balok adalah d = √(p² + l²), d = √(p² + t²), atau d = √(l² + t²).

Sedangkan untuk garis diagonal ruang pada balok memiliki satu panjang yang sama yaitu d = √(p² + l² + t²). Di mana p = panjang baok, l = lebar balok, dan t = tinggi balok.

Baca Juga: Materi dan Rumus pada Dimensi Tiga

3) Jarak Titik ke Titik pada Limas

Sebuah limas memiliki sisi tegak dengan bentuk segitiga. Sementara alasnya dapat berbentuk aneka macam. Untuk limas dengan alas berbentuk segi empat disebut limas segi empat. Untuk limas dengan alas berbentuk segi n disebut sebagai limas segi n.

Jarak titik puncak limas ke titik proyeksinya pada alas sama dengan tinggi limas. Jarak titik puncak limas ke setiap titik sudut pada alas limas sama dengan rusuk tegak limas.

Baca Juga: Rumus Volume dan Luas Permukaan Limas

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.

Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Jarak Titik ke Titik pada R3

Diketahui titik A dan titik G merupakan titik-titik sudut pada kubus ABCD.EFGH dengan panjang rusuk 5 cm. Jarak titik A ke titik G adalah ….
A. 5√3 cm
B. 5√2 cm
C. 5 cm
D. 3√5 cm

Pembahasan:
Sebuah segemn garis yang menghubungkan titik A ke titik G pada kubus ABCD.EFGH merupakan diagonal ruang kubus tersebut. Sehingga, jarak titik A ke titik G pada kubus ABCD.EFGH sama dengan panjang diagonal ruang kubus yaitu 5√3 cm.

Jadi, jarak titik A ke titik G adalah 5√3 cm.

Jawaban: A

Baca Juga: Jarak Garis ke Bidang pada Dimensi Tiga

Contoh 2 – Soal Jarak Titik ke Titik pada Balok

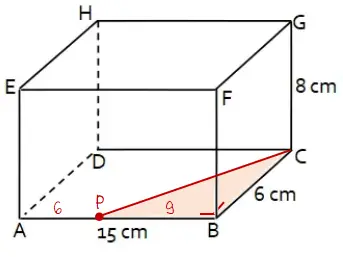
Perhatikan gambar balok berikut!

Titik P terletak pada garis AB dengan AP : PB = 2 : 3. Jarak titik P ke titik C adalah ….
A. 3√29 cm
B. 3√17 cm
C. 6√3 cm
D. 6√2 cm
E. 3√13 cm

Pembahasan:
Dari gambar dapat diketahui bahwa panjang ruas garis AB = 15 cm dan perbandingan panjang ruas garis AP dan PB adalah 2 : 3.

Panjag ruas garis AP dan PB dapat dihitung dengan perbandingan senilai seperti berikut.

Diperoleh panjang AP = 6 cm dan BP = 9 cm. Selanjutnya, panjang BP digunakan untuk menghitung panjang garis CP = jarak titik C ke titik P.

Menghitung panjag CP:
CP² = BP² + BC² = 9² + 6² 
CP² = 81 + 36 = 117
CP = √117 = √(9×13)
CP = √9 × √13 = 3√13

Jadi, jarak titik P ke titik C adalah CP = 3√17 cm.

Jawaban: B

Contoh 3 – Soal Jarak Titik ke Titik pada Limas

Perhatikan limas T.KLMN berikut!

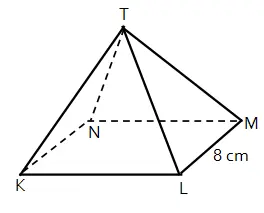
Diketahui alas limas berbentuk persegi. Jika tinggi limas 4 cm, jarak titik T ke titik M adalah ….
A. 4√6 cm
B. 3√6 cm
C. 2√6 cm
D. 4√3 cm
E. 4√2 cm

Pembahasan:
Alas limas KLMM memiliki bentuk persegi, sehingga panjang diagonal KM = rusuk√2 = 8√2 cm. Tinggi limas adalah TO = 4 cm di mana titik O merupakan titik tengah diagonal pada alas limas. Sehingga panjang MO = KO = ½ × 8√2 = 4√2 cm.

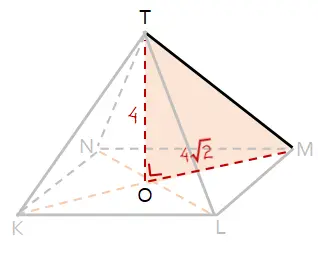
Perhatikan segitiga TOM dalam limas T.KLMN! Segitiga tersebut merupakan segitiga siku-siku. Diketahui panjang TO = 4 cm dan MO = 4√2 cm. Panjang TM dapat diketahui dengan rumus pada Teorema Pythagoras.

Menghitung panjang TM:
TM² = TO² + MO² 
TM² = 4² + (4√2)² 
TM² = 16 + 32 = 48
TM = √48 = √(16×3)
TM = √16 × √3 = 4√3 cm

Jadi, jarak titik T ke titik M adalah TM = 4√3 cm.

Jawaban: D

Demikianlah tadi ulasan jarak titik ke titik pada dimensi tiga (R3). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!