Vektor adalah ruas garis berarah yang memiliki nilai panjang dan arah. Besaran vektor merupakan jenis besaran yang memiliki nilai dan arah. Contoh besaran vektor adalah perpindahan, kecepatan, percepatan, dan besaran lain yang memiliki nilai serta arah. Panjang vektor v merupakan jarak dari titik pangkal ke titik ujung dan ditulis dalam simbol |v|. Sebuah besaran vektor dapat dinyatakan dengan huruf kapital dengan cetak tebal seperti A atau dapat juga ditulis dengan sebuah huruf dan tanda panah pada bagian atas huruf.
Vektor digambarkan sebagai ruas garis dari titik pangkal ke titik ujung dengan tanda panah pada bagian ujung vektor. Vektor R pada bidang kartesius menyatakan perpindahan titik dari a ke b. Dua vektor dikatakan sama jika panjang dan arahnya sama. Operasi hitung penjumlahan dapat dilakukan pada dua buah vektor atau lebih. Cara melakukan operasi penjumlahan vektor dapat dilakukan dengan beberapa metode. Ada 4 metode penjumlahan vektor yaitu metode segitiga, jajar genjang, poligon, dan analitis.

Bagaimana cara penjumlahan vektor dengan empat metode tersebut? Apa perbedaanya? Sobat idschool dapat menyimak lebih lanjut bahasan keempat metode penjumlahan vektor pada ulasan di bawah.
Baca Juga: Perbandingan Vektor
Penjumlahan Vektor Metode Segitiga
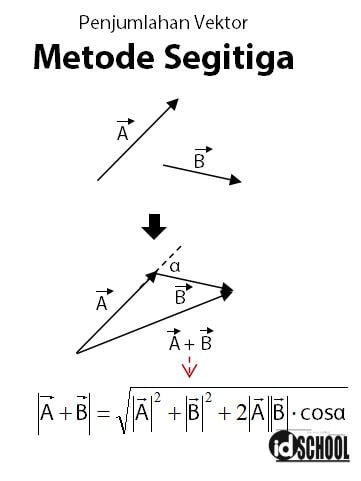
Penjumlahan vektor metode segitiga dilakukan pada dua buah vektor yang hasilnya merupakan penjumlahan kedua vektor tersebut. Misalnya pada penjumlahan dua buah vektor yaitu vektor A dan vektor B. Penjumlahan vekor A dan vektor B dilakukan dengan cara menyambung ujung vektor A dengan pangkal vektor B.
Hasil penjumlahan kedua vektor sama dengan vektor yang terbentuk dengan menghubungkan ujung pangkal vektor A dan ujung vektor B. Dua vektor yang dijumlahkan dan hasil penjumlahan membentuk bangun segitiga. Sehingga, metode penjumlahan ini disebut sebagai penjumlahan vektor metode segitiga. Panjang vektor hasil penjumlahan dapat dihitung melalui persamaan |A + B|2 = |A|2 + |B|2 + 2|A||B| · cos α, dengan α merupakan sudut yang terbentuk oleh kedua vektor yang dijumlahkan.
Baca Juga: Vektor Posisi dan Penyajian Vektor
Penjumlahan Vektor Metode Jajar Genjang
Penjumlahan dua buah vektor A dan vektor B dengan metode jajar genjang dilakukan dengan cara menyatukan pangkal kedua vektor A dan B. Kemudian dari titik ujung vektor A ditarik garis sejajar dengan vektor B, dan dari titik ujung vektor A ditarik garis sejajar dengan vektor B. Hasil penjumlahan kedua vektor tersebut adalah vektor yang diperoleh dengan menghubungkan titik pangkal ke titik perpotongan kedua garis sejajar tersebut. Panjang vektor hasil penjumlahan dapat dihitung menggunakan persamaan |A + B|2 = |A|2 + |B|2 + 2|A||B| · cos α, di mana α adalah sudut yang terbentuk oleh kedua vektor yang dijumlahkan.

Sama seperti pada metode sebelumnya, pada metode ini terbentuk bangun jajar genjang. Sehingga, penjumlahan vektor dengan metode ini disebut dengan metode jajar genjang.
Metode Poligon
Metode penjumlahan vektor selanjutnya adalah metode poligon. Penjumlahan vektor dengan metode poligon dapat dilakukan untuk beberapa vektor dengan cara menggambar. Sebuah vektor dijadikan sebagai acuan dan vektor lain disambungkan dengan pangkal tepat pada ujung vektor sebelumnya. Resultan vektornya dapat dibentuk dengan menggambar anak panah dari pangkal awal hingga ujung akhir.
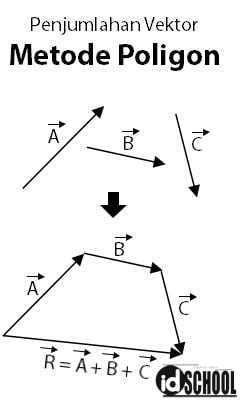
Poligon adalah sebutan untuk bagun dengan segi banyak. Penjumlahan vektor dengan metode poligon akan membentuk suatu bangun dengan segi banyak. Banyaknya sisi poligon tergantung banyaknya vektor yang terlibat. Semakin banyak vektor yang dijumlahkan, sisi bangun poligon akan semakin banyak pula.
Metode Analitis
Metode analitis untuk menjumlahkan vektor dilakukan tanpa perlu menggambar vektor terlebih dahulu. Penjumlahan dengan metode analisis dilakukan dengan menguraikan vektor pada bidang sumbu melalui proyeksi. Hasil proyeksi vektor berupa komponen vektor yang terletak pada sumbu suatu bidang.
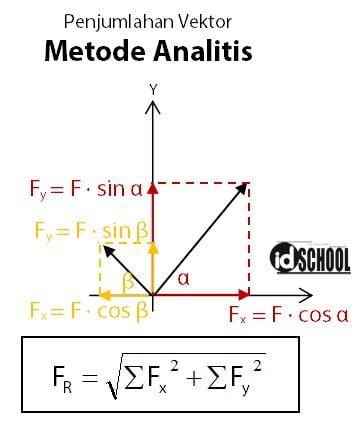
Misalnya, sebuah vektor terletak pada bidang kartesius pada R2. Proyeksi vektor akan menghasilkan komponen vektor pasa sumbu x dan sumbu y. Nilai komponen vektor F pada sumbu X adalah Fx = F·cos α, sedangkan nilai komponen F pada sumbu Y adalah Fy = F·sin α. Di mana, α merupakan sudut yang dibentuk suatu vektor dengan sumbu X.
Resultan vektor pada penjumlahan dengan metode analisis dapat dihitung dengan persamaan FR2 = ∑Fx2 + ∑Fy2. Di mana, FR adalah resultan/hasil penjumlahan vektor, Fx adalah komponen vektor pada sumbu x, dan Fy adalah komponen vektor pada sumbu y.
Baca Juga: Cara Menghitung Resultan Vektor 3 Arah Secara Analitis
Contoh Soal dan Pembasahan
Sobat idschool dapat melatih pemahaman materi di atas dengan cara berlatih mengerjakan soal. Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menampah pemahaman. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Pembahasan soal yang diberikan
Contoh 1 – Soal Penulisan Vektor yang Benar
Perhatikan gambar berikut!

Dari susunan vektor-vektor tersebut, penulisan vektor yang benar adalah ….
A. Z = W + X + Y
B. W + Z = X + Y
C. Y + Z = W + X
D. X = W + Y + Z
E. Y = W + X + Z
Pembahasan:
Hasil penjumlahan vektor terdapat pada vektor dengan pangkal dan ujung vektor saling bertemu dengan vektor lain. Berdasarkan gambar pada soal, pangkal vektor Z bertemu dengan pangkal vektor W dan ujung vektor Z bertemu ujung vektor Y. Sedangkan ketiga vektor lainnya saling menyambung antara pangkal dengan ujung vektor lainnya.
Kesimpulannya, Z merupakan vektor hasil penjumlahan dari vektor W, X, dan Y atau Z = W + X + Y + Z.
Jawaban: A
Contoh 2 – Soal Penulisan Vektor
Perhatikan gambar vektor-vektor di bawah!

Pernyataan yang benar berdasarkan gambar di atas adalah ….
A. P + Q + R = S
B. P + Q + S = R
C. Q + R + S = P
D. P + Q + R = –P
E. Q + R – S = P
Pembahsan:
Hasil penjumlahan vektor terdapat pada vektor dengan pangkal dan ujung vektor saling bertemu dengan vektor lain. Berdasarkan gambar pada soal, pangkal vektor P bertemu dengan pangkal vektor Q dan ujung vektor P bertemu ujung vektor S. Sedangkan ketiga vektor lainnya yaitu Q, R, dan S saling menyambung antara pangkal dengan ujung vektor lainnya.
Jadi, P merupakan vektor hasil penjumlahan dari vektor Q, R, dan S atau Q + R + S = P.
Jawaban: C
Baca Juga: Perkalian Vektor
Contoh 3 – Soal Mencari Sudut yang Dibentuk Dua Vektor
Vektor a = 3 satuan, vektor b = 4 satuan dan vektor a – vektor b = 5 satuan, besar sudut yang diapit oleh vektor a dan b adalah ….
A. 90o
B. 45o
C. 60o
D. 120o
E. 180o
Pembahasan:
Deikrtahui:
- vektor a: A = 3 satuan
- vektor b: B = 3 satuan
- Vektor a – vektor b = A – B = 5 satuan
Menghitung sudut yang dibentuk vektor a (A) dan vektor b (B):
|A – B|2 = |A|2 + |B|2 – 2|A||B|·cos α
52 = 32 + 22 – 2(3)(2)·cos α
25 = 13 – 12 · cos α
25 – 13 = –12 · cos α
12 = –12 · cos α
cos α = –12/12
cos α = –1
α = 180o
Jadi, besar sudut yang diapit oleh vektor a dan b adalah 180o.
Jawaban: E
Demikianlah tadi ulasan 4 metode penjumlahan vektor yang meliputi metode segitiga, jajar genjang, poligon, dan analitis. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Perbedaan Kelajuan dan Kecepatan
