Cara mengetahui besar sudut antara 2 garis pada kubus ABCD.EFGH dapat dilakukan melaui persamaan fungsi trigonometri. Di mana persamaan bentuk dasar dari fungsi trigonometri antara lain meliputi fungsi sinus (sin), cosinus (cos), dan cotangen (tan). Ketiga fungsi trigonometri menyatakan bagaimana hubungan besar sudut dalam segitiga dengan panjang sisi-sisi segitiga.
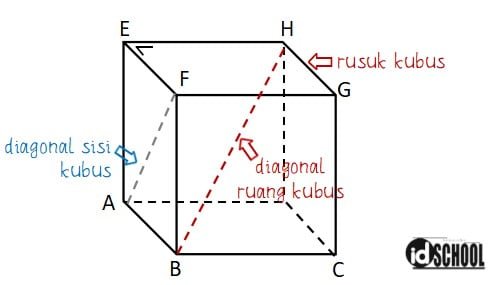
Kubus ABCD.EFGH adalah salah satu bangun ruang yang memiliki 6 sisi dan 12 rusuk. Bidang sisi pada kubus memiliki bentuk dan ukuran yang sama dan panjang rusuk berupa ruas garis yang sama panjangnya. Setiap rusuk pada kubus yang saling berpotongan membentuk sudut 90o (siku-siku). Kubus memiliki ruas garis diagonal sisi pada setiap bidang sisi. Kubus juga memiliki ruas garis berupa diagonal ruang yang menghubungkan dua titik pada kubus dengan jarak paling jauh.
Baca Juga: Cara Menentukan Letak dan Besar Sudut Antara Bidang dan Bidang pada Kubus ABCD.EFGH
Antara dua ruas garis pada kubus berupa rusuk, digonal sisi, diagonal ruang, dan ruas garis lain dapat membentuk suatu besar sudut. Bagaimana cara menentukan letak sudut antara 2 garis pada kubus ABCD,EFGH? Bagaimana cara menentukan besar sudut antara 2 garis? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Letak Sudut Antara 2 Garis pada Kubus ABCDEFGH
- Cara Menghitung Besar Sudut Antara 2 Garis pada Kubus ABCD.EFGH
- Contoh Soal dan Pembahasan
Letak Sudut Antara 2 Garis pada Kubus ABCDEFGH
Pada kubus ABCD.EFGH terdapat garis yang saling sejajar, berpotongan, dan bersilangan. Letak sudut antara 2 garis terdapat pada dua garis yang memiliki titik potong. Sudut yang terbentuk antara dua garis terdapat pada daerah antara perpotongan kedua garis tersebut.
Jika diketahui 2 garis tidak berpotongan (tidak memiliki potong) maka salah satu garis atau keduanya perlu digeser terlebih dahulu. Penggeseran garis dilakukan dengan arah sejajar dengan letak garis awal. Tujuan dari penggeseran garis dilakukan agar kedua garis memiliki titik potong (berpotongan).
Contoh garis pada kubus ABCD.EFGH yang memiliki titik potong dan tidak memiliki titik potong.
Baca Juga: Jarak 2 Garis Bersilangan pada Suatu Bangun Ruang
Cara Menghitung Besar Sudut Antara 2 Garis pada Kubus ABCD.EFGH
Besar sudut antara 2 garis sejajar pada kubus ABCD.EFGH adalah 0o. Untuk besar sudut pada dua garis yang saling berpotongan dapat langsung dicari melalui persamaan fungsi trigonometri.
Sedangkan untuk dua garis yang saling bersilangan perlu membuat kedua garis berpotongan terlebih dahulu. Caranya dengan menggeser salah satu garis atau kedua garis sehingga memiliki titik potong.
Dua ruas garis yang mengapit sudut dan sebuah ruas garis yang berhadapan dengan sudut akan membentuk sebuah segitiga. Ada beberapa kemungkinan segitiga yang dapat terbentuk antara lain segitiga siku-siku, sama sisi, siku-siku sama kaki, dan segitiga sembarang.
Jika segitiga yang terbentuk adalah segitiga sama kaki maka besar sudut yang terbentuk sama dengan 60o. Kondisi ini sesuai dengan sifat pada segitiga sama kaki yang ketiga sudutnya sama dengan 60o. Sebagai contoh adalah antara dua buah diagonal sisi pada kubus ABCD.EFGH memiliki besar sudut α = 60o.
Jika segitiga yang terbentuk adalah segitiga siku-siku sama kaki maka besar sudut yang terbentuk antara dua garis sama dengan 45o. Di mana pada segitiga siku-siku sama kaki memiliki dua panjang garis yang sama. Besar sudut tersebut diperoleh dari perbandingan tan α = 1 yang menghasilkan nilai besar sudut α = 45o. Besar sudut antara dua garis yang memiliki besar α = 45o terdapat pada contoh berikut.
Untuk segitiga yang dibentuk berupa segitiga siku-siku, besar sudut dapat ditentukan melalui fungsi trigonometri. Di mana fungsi sin merupakan perbandingan antara panjang sisi depan dan sisi miring. Fungsi cos merupakan perbandingan antara panjang sisi samping dan sisi miring. Sedangkan fungsi tan sama dengan perbandingan fungsi depan dan sisi samping.
Jika segitiga yang dihasilkan bukan segitiga siku-siku atau segitga tidak beraturan maka besar sudut dapat dicari dengan aturan cosinus.
Baca Juga: Kumpulan Berbagai Bentuk Soal dan Pembahasan Cara Menghitung Median Data Kelompok
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan rumus besar sudut antara 2 garis pa kubus. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan cara menghitung besar sudut antara 2 garis pada kubus. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Cara Menentukan Besar Sudut Antara 2 Garis
Diketahui kubus ABCD.EFGH memiliki panjang rusuk sama dengan 6 cm. Besar sudut antara garis AH dan EG adalah ….
A. 30o
B. 45o
C. 60o
D. 90o
E. 120o
Pembahasan:
Antara garis AH dan EG tidak memiliki titik potong sehingga besar sudut dicari dengan menggeser salah satu garis dengan arah sejajar agar berpotongan. Garis EG sejajar dengan garis AC dan garis AC berpotongan dengan garis AH di titik C. Sudut yang dibentuk antara 2 garis pada kubus ABCD.EFGH tersebut adalah sudut HAC.
Letak sudut antara garis AH dan AC ditunjukkan seperti pada gambar berikut.
Perhatikan segitiga HAC yang dibentuk oleh garis AH, AC, dan HC. Ketiga garis yang mebentuk segitiga HAC memiliki panjang yang sama berupa diagonal sisi. Sehingga segitiga HAC merupakan segitiga sama sisi. Besar ketiga sudut pada segitiga sama sisi adalah 60o, sehingga besar ∠HAC = 60o.
Besar sudut antara garis AH dan EG adalah sama dengan besar ∠HAC = 60o. Jadi, besar sudut antara garis AH dan EG adalah 60o.
Jawaban: C
Contoh 2 – Soal Besar Sudut Antara 2 Garis
Pembahasan:
Garis yang sejajar dengan BF dan berpotongan dengan garis HC adalah garis CG yang berpotongan pada titik C. Kedua garis tersebut dan garis HG membentuk sebuah segitiga sama kaki yaitu segitiga HCG. Di mana sudut HCG merupakan sudut antara garis HC dan garis CG.
Diketahui bahwa sisi depan dan sisi samping segitiga HCG sama dengan panjang rusuk kubus. Jika besar sudut antara garis HC dan CG adalah α maka tan α = 1 sehingga α = 45o. Sehingga dapat diperoleh bahwa besar sudut antara garis HC dan CG adalah α = 45o.
Besar sudut antara 2 garis tersebut nya sama dengan sudut antara garis HC dan garis BF. Jadi, besar sudut antara garis HC dan garis BF pada kubus
ABCD.EFGH di samping adalah α = 45o.
Jawaban: C
Demikianlah ulasan cara menentukan besar sudut antara 2 garis yang disertai dengan contoh soal dan pembahasan. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menentukan Determinan Matriks 3×3