Vektor adalah objek geometri yang dan memiliki nilai dan arah. Sebuah vektor a memiliki titik pangkah A dan titik ujung B. Disebut juga sebagai vektor AB. Panjang vektor AB sama dengan jarak terpendek titik A ke titik B.
Sebuah vektor memiliki bentuk anak panah (→). Pangkal anak panah adalah titik awal vektor. Sedangkan ujung anak panah merupakan titik akhir vektor. Panjang sebuah vektor sama dengan jarak terpendek pangkal ke ujung anak panah.
Rumus hitung panjang vektor dan caranya ada di bawah.
Daftar isi:
Rumus Panjang Vektor AB
Panjang vektor disimbolkan dengan huruf kecil yang diapit tanda lurus. Bentuknya seperti nilai mutlak. Misalnya vektor v, panjang vektornya adalah |v|. Untuk vektor AB, panjang vektornya adalah |AB|. Rumus dan cara menghitung panjang vektor ada di bawah.
Diketahui persamaan vektor
Vektor yang besarnya sama dengan 1 disebut vektor satuan. Pada sistem koordinat kartesius xyz, vektor satuan dinyatakan i, j, dan k. Vektor satuan i menaytakan arah sumbu x positif. Vektor satuan j menyatakan arah sumbu y negatif. Dan vector satuan k menyatakan arah sumbu z positif.
Persamaan vektor menyatakan arah vektor pada sumbu x, y, dan z. Misalnya vektor u memiliki arah dua satuan ke kanan dan tiga satuan ke atas. Persamaan vektor tersebut adalah u = 2i + 3j.
Untuk vektor tiga dimensi, misalnya vektor v yang memilki arah 3 satuan pada sumbu x, 2 sataun pada sumbu y, dan 1 satuan pada sumbu z. Persamaan vektor tersebut adalah v = 3i + 2y + z.
Secara umum, persamaan vektor dua dimensi adalah u = ai + bj. Dan persamaan vektor tiga dimensi adalah v = pi + qy + rz. Rumus panjang vektor sama dengan akar dari kuadrat bilangan-bilangan penyusun vektor.

Cara menghitungnya ada pada langkah penyelesaian soal di bawah.
Soal:
Tentukan panjang vektor a = 2i + 4j!
Jawab:
Mengghitung panjang vektor a:
|a| = √(22 + 42)
= √(4 + 16) = √20
= √(4×5) = √4 × √5 = 2√5
Jadi, panjang vektor a adalah 2√5 satuan panjang.
Diketahui titik koordinat ujung dan pangkal vektor
Diketahui vektor letak yang titik koordinat ujung dan pangkalnya adalah A(x1, y1) dan B(x2, y2). Perpotongan garis proyeksi titik A dan B membentuk segitiga siku-siku. Panjang vektor ini dihitung menggunakan rumus Pythagoras.
Persamaan untuk menghitung panjang vektor AB adalah |AB|2 = (x2 – x1)2 + (y2 – y1)2.

Contoh cara menghitung panjang vektornya ada di bawah.
Soal:
Tiga buah vektor membentuk segitiga ABC.
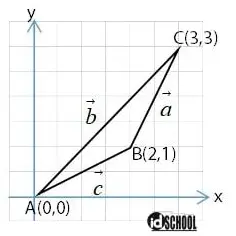
Koordinat titik sudut segitiga ABC adalah A(0, 0); B(2,1); dan C(3, 2). Panjang vekor c adalah ….
Jawab:
Panjang vektor c sama dengan panjang ruas garis AB. Cara menghitungnya dapat menggunakan rumus Pythgoras seperti berikut.
Menghitung panjang vektor c:
|c| = |AB|
= √[(2 – 0)2 + (1 – 0)2]
= √(22 + 12) = √(4 + 1) = √5
Jadi, panjang sisi AB sama dengan panjang vektor c yaitu √5 satuan panjang.
Baca Juga: Perbandingan Vektor
Contoh Soal dan Pembahasan
Latihan soal panjang vektor AB ada di bawah.
Contoh 1 – Soal Panjang Vektor AB
Diketahui letak titik A(3, –1, 2) dan letak titik B (5, 4, 1). Besar panjang vektor AB adalah ….
A. 30
B. √30
C. 10√3
D. 3√10
E. 3
Pembahasan:
Komposisi bilangan untuk vektor AB:
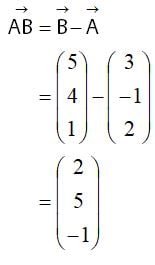
Menghitung besar panjang vektor AB:
|AB| = √(22 + 52 + (–1)2)
= √(4 + 25 + 1)
= √30
Jadi, panjang vektor AB adalah √30 satuan panjang.
Jawaban: B
Contoh 2 – Soal Panjang Vektor
Diketahui vektor-vektor a, b, dan c dengan vektor b = (−2,1), vektor b ⊥ vektor c, vektor a − b + c = 0. Jika luas segitiga yang dibentuk ujung-ujung vektor a, vektor b, dan, vektor c adalah √5, maka panjang vektor a adalah ….
A. √2
B. 2
C. √3
D. √6
E. 3
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
Vektor b = (−2, 1)
Panjang vektor b: |b| = √(–22 + 12) = √5
vektor b ⊥ vektor c → b · c = 0
a − b + c = 0 → a = b − c
Luas segitiga ABC = √5
Gambar yang sesuai dengan kondisi pada soal diberikan seperti berikut.

Menghitung panjang OC (c):
L∆ABC = 1/2 × L∆OABC = 1/2×OC×OB
√5 = 1/2 × OC × √5
1 = 1/2 × OC
OC = 2
Menghitung panjang vektor a:
|a|2 = |b – c|2 = |b|2 + |c|2 – 2·|b|·|c| · cos 90o
|a|2 = √52 + 22 – 2·√5·2 · 0 = √52 + 22 – 0 = 9
Sehingga,
|a| = √9 = 3
Jadi, panjang vektor a adalah |a| = 3 satuan panjang.
Jawaban: E
Demikianlah ulasan cara menghitung panjang vektor AB. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Metode Penjumlahan Vektor
