Sistem persamaan linear (SPL) adalah beberapa persamaan linear yaitu suatu persamaan yang memiliki variabel dengan pangkat tertinggi sama dengan 1. Cara menyelesaikan SPL dengan matriks dapat menjadi alternatif penyelesaian sistem persamaan linear yang memiliki banyak varibel. Ada beberapa cara untuk menyelesaikan sistem persamana linear antara lain metode subtitusi, eliminasi, dan campuran. Selain itu cara menyelesaikan sistem persamaan linear dengan matriks juga dapat digunakan. Penyelesaian sistem persamaan linear berupa nilai-nilai varibel yang memenuhi semua persamaan dalam sistem persamaan linear.
Matriks sendiri adalah susunan bilangan-bilangan dalam baris dan kolom, di mana baris dan kolom matrik menyatakan ukuran matriks. Misalnya suatu matriks diketahui memiliki ukurab 3 x 3, artinya matriks tersebut terdiri atas tiga baris dan tiga kolom. Isi baris dan kolom pada matriks adalah bilangan-bilangan, sehingga pada matriks dengan ukuran 3 x 3 memuat 9 bilangan. Contoh lain, matriks dengan ukuran 2 x 3 artinya matriks memiliki dua baris dan tiga kolom. Berbeda dengan matriks dengan ukuran 3 x 2 yang artinya matriks memiliki tiga baris dan dua kolom.
Baca Juga: Operasi Hitung pada Matriks
Suatu bentuk sistem persamaan linear dapat dibawa ke dalam bentuk matriks. Dari bentuk matriks yang diperoleh kemudian dapat diselesaikan sehingga diperoleh nilai-nilai dari variabel yang memenuhi sistem persamaan linear. Itulah salah satu fungsi dari matriks yaitu untuk menyelesaikan SPL dengan matriks.
Bagaimana cara mebentuk sistem persamaan linear ke dalam bentuk matriks? Bagaimana cara menyelesaikan sistem persamaan linear (SPL) dengan matriks? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Cara Menyelesaikan SPL dengan Matriks untuk 2 Variabel
Cara yang paling umum dilakukan untuk menyelesaikan sistem persamaan linear dua variabel (SPLDV) adalah menggunakan metode substitusi, eliminasi, atau campuran. Kali ini, idschool akan mengenalkan cara menyelesaiakan sistem persamaan linear (SPL) dengan cara yang baru, yaitu dengan menggunakan matriks. Meskipun cara ini akan sedikit rumit, namun cara ini akan sangat berguna untuk menyelesaikan sistem persamaan linear dengan banyak variabel.
Diketahui sistem persamaan linear dengan dua varibel yaitu ax + by = c dan px + qy = r. Bentuk sistem persamaan linear dua varibel tersebut dapat ditulis dalam bentuk matriks seperti berikut.
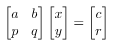
Berdasarkan sifat matriks invertibel, maka variabel x dan y dapat diketahui melalui cara berikut.

Selain cara di atas, penyelesaian matriks untuk mendapatkan nilai x dan y juga dapat dilakukan dengan nilai determinan matriks (D).

Contoh cara menyelesaikan SPL dengan matriks pada sistem persamaan linear dengan dua variabel dapat dilihat seperti pada pembahasan di bawah.
Soal:
Tentukan nilai x dan y yang memenuhi sistem persamaan linear 2x + y = 5 dan x + y = 7!
Penyelesaian:
Bentuk matriks yang sesuai dengan sistem persamaan linear 2x + y = 5 dan x + y = 7 adalah sebagai berikut.
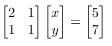
Dengan menyelesaikan operasi matriks untuk variabel x dan y di ruas kiri dan yang lain di ruas kanan maka selanjutnya dapat diperoleh nilai x dan y. Cara menyelesaikan SPL dengan matriks untuk soal seperti di atas dapat diselesaikan seperti cara berikut.

Jadi, solusi dari dua persamaan linear dua variabel 2x + y = 5 dan x + y = 7 adalah x = –2 dan y = 9.
Baca Juga: Pengertian Matriks dan Sifat-Sifatnya
Menyelesaikan SPLTV dengan Matriks
Cara menyelesaikanSPL dengan matriks akan sangat bermanfaat pada sistem persamaan linear dengan variabel yang banyak, misalnya pada sistem persamaan linear tiga variabel (SPLTV). Metode substitusi, eliminasi, atau campuran dirasa tidak tepat untuk menyelesaikan SPLTV.
Selanjutnya, simak penyelesaian sistem persamaan linear tiga variabel (SPLTV) menggunakan matriks.
Diketahui tiga persamaan linear dengan tiga variabel (x, y, dan z):
ax + by + cz = d
px + qy + rz = s
kx + ly + mz = n
Bentuk SPLTV di atas dalam bentuk matriks dapat dibuat seperi berikut.
Baca Juga: Cara Menentukan Invers Matriks
Berdasarkan matriks di atas, dapat disusun determinan utama, determinan variabel x, determinan variabel y, dan determinan variabel z. Untuk lebih jelasnya perhatikan masing-masing determinan pada daftar di bawah.
- Determinan utama

- Determinan variabel x

- Determinan variabel y

- Determinan variabel z

Selanjutnya, nilai dari ketiga variabel yaitu x, y, dan z dapat dihitung melalui persamaan di bawah.
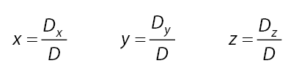
Sekian materi mengenai cara menyelesaikan sistem persamana linear (SPL) dengan matriks. Terimakasih sudah mengunjungi idschool(dot)net. Semoga Bermanfaat!
Baca Juga: Transpose Matriks dan Sifat-sifat Transpose Matriks





???????????? mana lagi