Kerucut merupakan bangun ruang dengan alas berbentuk lingkaran. Jumlah sisi pada kerucut ada dua, yaitu sebuah sisi alas berbentuk lingkaran dan sebuah sisi lengkung yang menjadi selimut. Jika kerucut diiris dari berbagai arah, hasil irisannya akan membentuk beberapa bangun. Hasil bangun dari irisan kerucut dapat berbentuk lingkaran, elips, parabola, atau hiperbola.
Sebuah kerucut yang dipotong secara mendatar akan menghasilkan potongan kerucut berupa lingkaran. Kerucut yang dipotong dengan arah sudut tertentu akan membentuk elips atau parabola. Potongan secara tegak menghasilkan bangun hiperbola. Berikut ini adalah gambar kerucut yang dipotong dari beberapa arah sehingga menghasilkan lingkaran, elips, parabola, dan hiperbola.

Pembahasan lainnya secara lebih lengkap dapat disimak pada uraian materi di bawah.
Table of Contents
Lingkaran
Bentuk potongan irisan kerucut jika dipotong sebuah bidang dengan arah mendatar adalah lingkaran. Pembahasan materi irisan kerucut berupa bentuk lingkaran meliputi bentuk umum persamaan lingkaran dengan jari-jari dan pusat yang berbeda.
Bentuk umum persamaan lingkaran dibedakan menjadi dua, yaitu berdasarkan pusat. Apakah pusat lingkaran berada di pusat koordinat kartesius O (0, 0) atau berada di suatu titik pada koordinat kartesius P(a, b). Selain itu, ada satu bentuk persamaan lingkaran yang diberikan dalam bentuk lain, yaitu x2 + y2 + Ax + By + C = 0. Simak ulasan persamaan rumus lingkaran lebih lengkapnya pada materi di bawah.
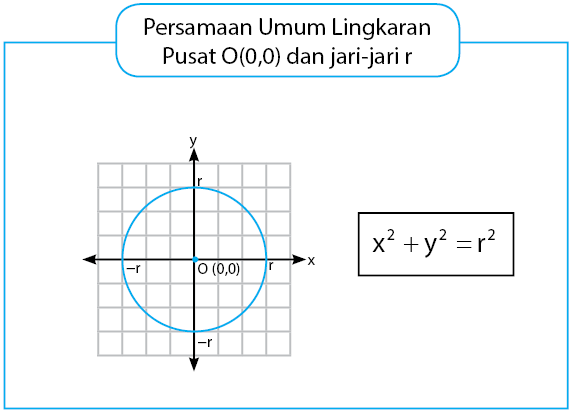
Persamaan lingkaran dengan pusat O(0, 0) dengan jari – jari r
Persamaan lingkaran dengan pusat P(a, b) dengan jari – jari r

Bentuk umum persamaan lingkaran:
Selain dua bentuk umum persamaan lingkaran yang telah diberikan di atas, ada juga bentuk umum persamaan lingkaran yang dapat digunakan untuk keduanya. Bentuk umum persamaan lingkaran tersebut adalah sebagai berikut.
Baca Juga: Kedudukan titik terhadap lingkaran
Elips
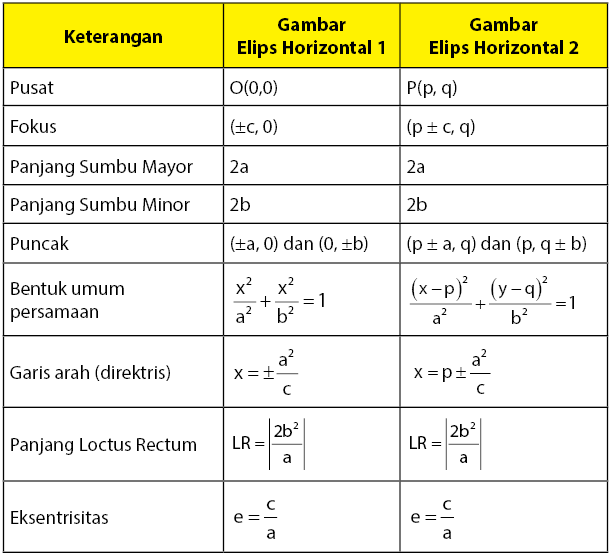
Hasil potongan dari irisan kerucut berikutnya yang akan dibahas adalah elips. Bentuk elips seperti lingkaran yang dipipihkan. Bagian-bagian elips yang penting untuk diketahui adalah sumbu mayor, sumbu minor, fokus elips, puncak elips, pusat elips, latus rectum, dan lain sebagainya. Elips dibedakan menjadi dua, yaitu elips horizontal dan elips vertikal.
Elips Horizontal

Perhatikan dua buah elips dengan dua pusat yang berbeda seperti pada gambar di bawah.

Berdasarkan dua elips di atas, akan diperoleh persamaan – persamaan di bawah.
Elips Vertikal

Berikut ini adalah dua gambar elips vertikal dengan pusat O dan P.

Berdasarkan dua elips di atas, akan diperoleh persamaan umum elips di bawah.

Pada elips, hubungan antara puncak dan fokus (hubungan a, b, dan c) memenuhi persamaan di bawah.
- Jika a > b (elips horizontal): a2 = b2 + c2
- Jika a < b (elips vertikal): b2 = a2 + c2
Baca Juga: Kedudukan titik pada elips
Parabola
Bentuk parabola menyerupai kurva mulus pada persamaan kuadrat. Materi parabola yang akan dibahas di sini meliputi parabola dengan bentuk terbuka ke atas atau ke bawah dan parabola dengan bentuk terbuka ke samping kanan atau kiri. Bentuk parabola ini sesuai dengan persamaan yang membentuknya. Parabola dapat dibedakan menjadi parabola horizontal dan vertikal.
Parabola dengan titik puncak O(0, 0)
Perhatikan dua bentuk parabola horizontal dan vertikal dengan titik puncak O(0,0) pada gambar di bawah.

Bentuk umum persamaan parabola, baik untuk parabola horizontal atau parabola vertikal adalah sebagai berikut.

Parabola dengan titik puncak P(a, b)
Perhatikan dua bentuk parabola horizontal dan vertikal dengan titik puncak P(a, b) pada gambar di bawah.

Bentuk umum persamaan parabola horizontal dan vertikal adalah sebagai berikut.

Baca Juga: Kedudukan titik pada parabola
Hiperbola
Hiperbola adalah bentuk irisan kerucut terakhir yang akan diulas. Komponen penyusun parabola adalah kurva, asimtot, garis arah (dirtektris), titik fokus, titik puncak, dan lain sebagainya. Semua komponen penyusun hiperbola saling berkaitan sehingga dapat dirumuskan sebuah persamaan umum.
Hiperbola horizontal dan vertikal beserta keterangannya terdapat pada gambar berikut.
- Hiperbola Horizontal

- Hiperbola Vertikal

Selanjutnya, akan diulas persamaan yang terdapat pada hiperbola dalam dua pembahasan. Pertama adalah hiperbola dengan pusat O(0, 0). Kedua adalah hiperbola dengan pusat P(a,b)
Hiperbola dengan pusat O(0, 0)
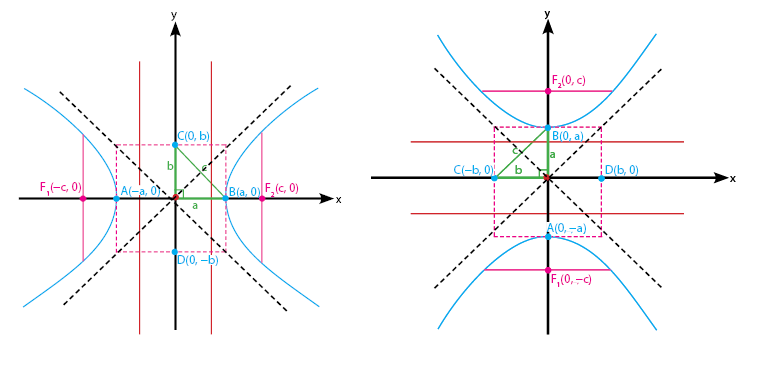
Berikut ini adalah rumus umum pada hiperbola dengan pusat O(0,0).

Hiperbola dengan pusat P(p, q)
Perhatikan dua bentuk hiperbola yang diberikan di bawah.

Rumus umum yang dapat digunakan sesuai dua gambar di atas dapat dilihat pada gambar di bawah.

Sekian pembahasan mengenai irisan kerucut yang meliputi lingkaran, elips, parabola, dan hiperbola. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Kedudukan Titik Terhadap Hiperbola


Saya bisa memahami dengan mudah se
Halo Fredi, terimakasih sudah mengunjungi idschool.