Kecepatan ayunan konis merujuk pada kecepatan benda yang bergerak dalam sistem ayunan konis. Ayunan konis adalah sebuah bandul bertali yang bergerak memutar sehingga seperti membentuk kerucut. Gerakan bandul yang membentuk kerucut membuat atunan konis juga dikenal dengan ayunan kerucut.
Lintasan yang dilalui bandul pada sistem gerak ayunan konis merupakan lingkaran yang merupakan bagian alas kerucut. Sehingga gerak melingkar bandul pada ayunan konis merupakan gerak melingkar horizontal. Gambaran gerak benda pada ayunan konis ditunjukkan seperti berikut.

Lintasan yang dilalui bandul dengan massa m berupa lingkaran yang merupakan alas kerucut. Titik ujung tempat tali bergantung merupakan titik puncak kerucut dan panjang tali merupakan garis pelukis kerucut. Sedangkan jari-jari kerucut R sama dengan jarak antara pusat (proyeksi titik puncak ke bagian alas kerucut) dan benda.
Benda dengan gerak melingkar mempunyai dua jenis kecepatan yaitu kecepatan sudut (ω) dan kecepatan linear (v). Besar kecepatan ayunan konis dapat dihitung melaui persamaan gaya yang bekerja pada sistem tersebut. Bagaimana persamaan yang dapat digunakan untuk menghitung kecepatan ayunan konis? Bagaimana penerapan analisis gerak pada ayunan kanonis pada peeristiwa sehari-hari? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Rumus Kecepatan Ayunan Konis
- Penerapan Analisis Gerak Ayunan Konis pada Gerak Mobil di Tikungan
- Contoh Soal dan Pembahasan
Baca Juga: Kumpulan Rumus untuk Benda dengan Gerak Melingkar Beraturan (GMB)
Rumus Kecepatan Ayunan Konis
Benda pada ayunan konis bergerak melingkar yang artinya terdapat gaya yang selalu menuju pusat lingkaran yaitu gaya sentripetal. Gaya sentripetal bukanlah gaya yang berdiri sendiri, melaikan resultan gaya yang bekerja pada benda dengan arah radial.
Rumus kecepatan gerak ayunan konis dapat diperoleh melalui persamaan yang dibentuk dari resultan gaya yang bekerja pada benda. Sebagai contoh, perhatikan penurunan rumus umum untuk mencari kecepatan kanonis seperti berikut.
Sebuah benda bermassa m diikatkan pada ujung seutas tali dengan panjang ℓ kemudian diputar dalam bidang horizontal dengan jari-jari R. Sudut yang terbentuk antara tali dan garis sumbu vertikal adalah α. Gaya-gaya yang bekerja pada benda tersebut diberikan seperti berikut.

Resultan gaya pada sumbu x: persamaan (1)
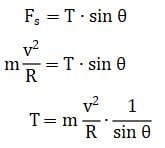
Resultan gaya pada sumbu y: persamaan (2)

Subsitusi T dari persamaan (1) dan (2) dapat diperoleh persamaan berikut.

Keterangan:
- g = percepatan gravitasi (m/s2)
- R = jari-jari lintasan melingkar (m)
- α = sudut yang terbentuk (o)
Baca Juga: Gaya dan Percepatan Sentripetal pada Benda dengan Gerak Melingkar
Penerapan Analisis Gerak Ayunan Konis pada Gerak Mobil di Tikungan
Analisis gerak pada ayunan konis dapat juga diterapkan untuk menyelesaikan beberapa masalah dalam kehidupan sehari-hari. Salah satu contoh penerapannya terdapat pada lintasan berupa tikungan yang dilalui mobil. Gerakan pada ayunan konis dan mobil pada tikungan sama-sama merupakan gerak melingkar horizontal. Kendaraan yang bergerak melingkar harus memiliki gaya sentripetal agar dapat melintas dengan aman.
Sebagai contoh:
Sebuah mobil bermassa 400 kg sedang melintasi belokan jalan yang melingkar dengan jari-jari 30 m dan dirancang dengan kemiringan 37o. Jika gaya gesek diabaikan maka berapakah kecepatan maksimum yang diperbolehkan mobil tersebut?
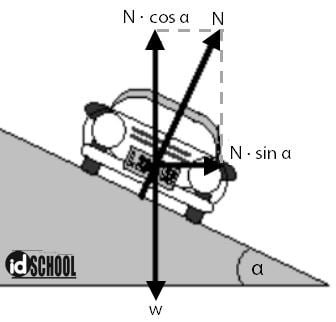
Keterangan yang diberikan pada soal:
- Massa mobil: m = 400 kg
- Jari-jari lintasan: R = 30 m
- Besar sudut yang dibentuk: α = 37o
Penyelesaian:
Pada arah vertikal (sumbu y), mobil tidak bergerak vertikal sehingga berlaku hukum I Newton dan dapat diperoleh persamaan berikut.
ΣF = 0
N cos 37o − w = 0
N × 0,8 − 400 × 10 = 0
0,8N = 4.000
N = 4.000/0,8 = 5.000 Newton
Pada arah horisontal (sumbu x) terdapat proyeksi N sin 37o, gaya tersebut bertindak sebagai gaya sentripetal. Sehingga, persamaan yang diperoleh diberikan seperti berikut.

Jadi, kecepatan maksimum yang diperbolehkan mobil tersebut adalah 15 m/s.
Baca Juga: Kecepatan Linear dan Anguler pada Benda dengan Gerak Melingkar
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara menghitung kecepatan ayunan konis. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Kecepatan Ayunan Konis dengan Gerak Melingkar
Ayunan konis diperlihatkan seperti pada gambar berikut!

Sebuah ayunan konis dengan benda bermassa 40 gram diputar menggunakan tali sepanjang 64 cm. Jika percepatan gravitasi 9,8 m/s2 maka kecepatan benda putar sebesar ….
A. 1,44 m/s
B. 1,68 m/s
C. 2,19 m/s
D. 3,21 m/s
E. 3,69 m/s
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informsi-informasi seperti berikut.
- Massa benda: m = 40 gram
- Panjang tali: R = 64 cm = 0,64 m
- Percepatan gravitasi: g = 9,8 m/s2
- Sudut yang terbentuk: α = 37o
Menghitung kecepatan benda putar:

Jadi, kecepatan benda putar sebesar 2,19 m/s.
Jawaban: C
Contoh 2 – Soal Kecepatan Ayunan Konis
Sebuah benda digantungkan pada seutas tali kemudian diputar mendatar seperti tampak pada gambar.

Jika panjang tali √2 meter dan α = 45o maka kecepatan putarannya adalah ….
A. 2,3 m/s
B. 3,2 m/s
C. 4,4 m/s
D. 5,5 m/s
E. 6,6 m/s
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Panjang tali: ℓ = √2 meter
- Sudut yang dibentuk: α = 45o
Menghitung kecepatan ayunan konis berupa gerak putaran benda:
v2 = g ⋅ R ⋅ tan α
= 10 × √2 × tan 45o
= 10√2 × 1/2√2 = 10
v = √10 ≈ 3,2 m/s
Jadi, putaran kecepatan ayunan konis tersebut sama dengan 3,2 m/s.
Jawaban: B
Baca Juga: Cara Mengetahui Besar Tegangan Tali yang Menarik Suatu Benda
Contoh 3 – Soal Besar Sudut yang Dibentuk pada Ayunan Konis
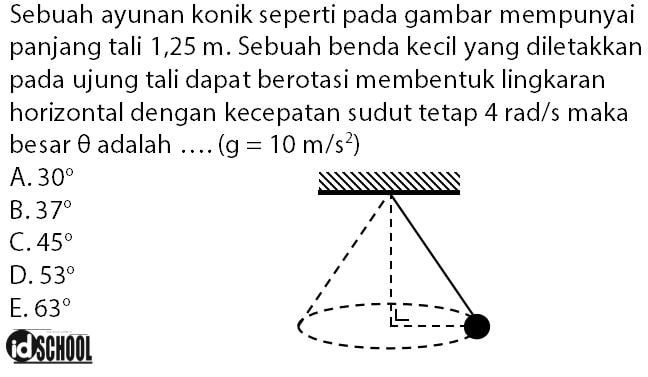
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Panjang tali: ℓ = 1,25 m
- Kecepatan sudut: ω = 4 rad/s
- Percepatan gravitasi: g = 10 m/s2
Menghithung besar θ:
v2 = g ⋅ R ⋅ tan θ
(ωR)2 = g ⋅ R ⋅ tan θ
ω2R2 = g ⋅ R ⋅ tan θ
ω2R = g ⋅ tan θ
42 × 1,25 = 10 × tan θ
20 = 10 × tan θ
tan θ = 20/10 = 2 → θ ≈ 63o
Jadi, besar θ adalah 63o
Jawaban: E
Demikianlah tadi ulasan materi putaran kecepatan ayunan konis pada benda dengan gerak melingkar. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Hubungan Roda – Roda (Sepusat, Bersinggungan, dan Dihubungkan Tali)
