Luas Daerah yang Dibatasi Kurva, Ada Cara Cepetnya Loh!

Rumus luas daerah yang dibatasi kurva adalah L = _a∫^b f(x) dx atau L = _a∫^b f(y) dy. Bentuk _a∫^b f(x) dx merupakan fungsi integral tentu. Rumus integral yang digunakan disesuaikan dengan daerah yang akan dicari luasnya.

Misalnya, sebuah daerah dibatasi oleh kurva f(x) = x² ‒ 16 dan sumbu x. Daerah yang dibatasi adalah daerah di bawah sumbu x. Batas daerahnya antara ‒4 sampai 4.

Ulasan lebih lanjut mengenai luas daerah yang dibatasi kurva ada di bawah.

Daftar isi:

• Rumus Luas Daerah yang Dibatasi Sebuah Kurva
  • 1) Dibatasi Sebuah Kurva dan Sumbu x
  • 2) Dibatasi Sebuah Kurva dan Sumbu y
• Luas Daerah yang Dibatasi 2 Kurva
  • 1) Batas integral pada sumbu x
  • 2) Batas integral pada sumbu y
• Contoh Soal dan Pembahasan
  • Contoh 1 – Luas daerah yang dibatasi kurva dan sumbu x
  • Contoh 2 – Luas daerah yang dibatasi lebih dari satu kurva
  • Contoh 3 – Menentukan rumus luas daerah yang dibatasi kurva

Rumus Luas Daerah yang Dibatasi Sebuah Kurva

Luas daerah tersebut dapat dihitung menggunakan fungsi integral. Mengapa? Karena luas daerah yang dicari sama dengan jumlah partisi daerah-daerahnya. Lihat penjelasan cara menghitung luas daerah yang dibatasi kurva untuk lebih jelasnya.

Ada dua rumus luas daerah yang dibatasi sebuah kurva. Ulasan kedua rumus luas tersebut ada di bawah.

1) Dibatasi Sebuah Kurva dan Sumbu x

Sebuah daerah dibatasi oleh sebuah kurva dan sumbu x. Jika luas daerah berada di atas sumbu x, rumus luasnya adalah L = _a∫^b f(x) dx. Jika daerah berada di bawah sumbu x, rumus luasnya adalah L = –_a∫^b f(x) dx.

Rumus luas daerah yang dibatasi sebuah kurva dan sumbu x:

Contohnya:

Soal 1:
Tentukan luas daerah yang dibatasi kurva y = x² ‒ 16 dan sumbu x!

Penyelesaian:
Untuk menghitung luas daerahnya, kita membutuhkan batas pengintegralan. Batas pengintegralan diperoleh dari titik potong garis dengan kurva.

Di sini, daerah yang akan dicari luasnya dibatasi oleh y = x² ‒ 16 dan sumbu x (y = 0). Sehingga batas pengintegralan adalah nilai x yang memenuhi persamaan x² ‒ 16 = 0.

Menentukan batas pengintegralan:

x² ‒ 16 = 0

(x ‒ 4)(x + 4) = 0

Diperoleh dua nilai x yang memenuhi yaitu x = 4 atau x = ‒4. Jadi, luas yang akan dicari memiliki batas pengintegralan ‒4 sampai 4.

Gambaran daerah yang akan dicari luasnya:

Baca Juga: Cara Menggambar Grafik Fungsi Kuadrat (Parabola)

Luas daerah yang dibatasi y = x² – 16 dan sumbu x berada di bawah sumbu x. Sehingga rumus yang digunakan adalah L = –_a∫^b f(x) dx.

Cara menghitung luas:

Luas = –_–4∫⁴ (x²–16) dx

Luas = [16x – ¹/₃x³]_–4⁴

Sehingga,

Luas = (16·4 – ¹/₃(4)³)–(16·(–4)–¹/₃(–4)³)

Luas = 64 – ⁶⁴/₃ + 64 – ⁶⁴/₃ = 85¹/₃ satuan luas

Jadi, luas daerah yang dibatasi y = x² – 16 dengan sumbu x adalah 85¹/₃ satuan luas.

RUMUS CEPATNYA!!

Rumus cepat menghitung luas daerah:

Keterangan: D = nilai diskriminan

Cara menggunakannya:

Daerah yang akan dicari luasnya dibatasi oleh kurva y = x² – 16 dan garis y = 0 (sumbu x). Samakan kedua persamaan tersebut. Sehingga diperoleh persamaan kuadrat x² – 16 = 0.

Persamaan kuadrat x² – 16 = 0 memiliki nilai a = 1, b = 0, dan c = 16. Sehingga nilai diskriminannya adalah D = b² – 4ac = 0² – 4 · 1 · (–16) = 64. Rumus luas daerah dengan cara cepat dihitung seperti berikut.

Diperoleh hasil yang sama dengan perhitungan sebelumnya, bukan?

2) Dibatasi Sebuah Kurva dan Sumbu y

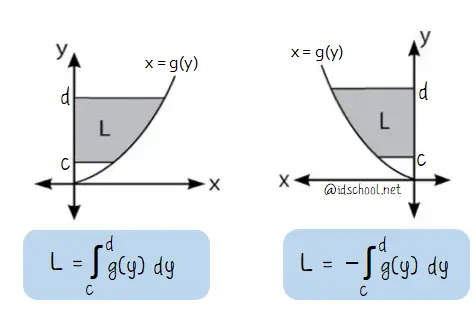
Sebuah daerah dibatasi oleh sebuah kurva dan sumbu y. Rumus luas daerahnya adalah L = _c∫^d f(y) dy jika daerah berada di kanan sumbu y. Untuk daerah yang berada di kiri sumbu x, rumus luasnya adalah L = –_c∫^d f(y) dy.

Rumus luas daerah yang dibatasi sebuah kurva dan sumbu y:

Contohnya:

Soal2:
Tentukan luas daerah tertutup yang dibatasi kurva f(x) = x², sumbu y, dan garis y = 4!

Penyelesaian:
Luas daerah pada soal ini menggunakan batas integral pada sumbu y. Batasnya ada dari 0 sampai 4.

HATI-HATI! Fungsi yang diketahui adalah f(x). Namun untuk perhitungan menggunakan fungsi f(y). Sehingga perlu dicari terlebih dahulu fungsi f(y)-nya.

Gambar luas daerah yang ada dicari:

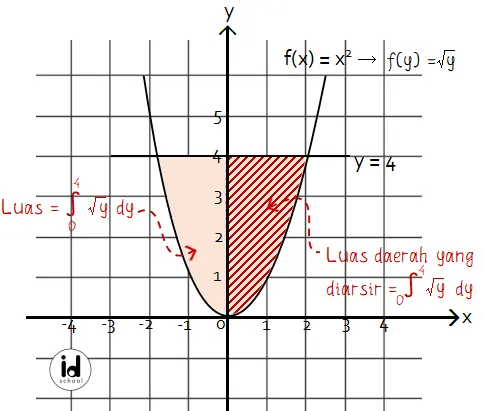
Daerah yang akan dicari luasnya berada di kanan sumbu y dan di kiri sumbu y. Untuk luas daerah yang beada di kanan sumbu y menggunakan rumus L = _a∫^b f(y) dy.

Untuk luas daerah yang disebelah kiri sumbu y sama dengan luas daerah di sebalah kanan. Sehingga luas totalnya dapat dihitung menggunkan rumus L = 2 × _a∫^b f(y) dy.

Rumus menghitung luas daerahnya:

Luas = 2 × ₀∫⁴ √y dy = 2 × ₀∫⁴ y^1/₂ dy

Sehingga,

Luas = 2ײ/₃(4)^3/2 = ⁴/₃ × √4³

Luas = ⁴/₃×√64 = ⁴/₃×8 = ³²/₃

Jadi, luas daerah tertutup yang dibatasi kurva f(x) = x², sumbu y, dan garis y = 4 adalah ³²/₃ satuan luas.

Luas Daerah yang Dibatasi 2 Kurva

Ada dua rumus yang bisa digunakan untuk menghitung luas daerah oleh dua kurva. Pertama saat batas integral menggunakan selang pada sumbu x. Kedua saat batas integral menggunakan selang pada sumbu y.

Rumus keduanya dijelaskan di bawah.

1) Batas integral pada sumbu x

Misalkan, sebuah daerah dibatasi oleh fungsi f(x) dan fungsi g(x). Luas daerah yang dibatasi oleh kedua fungsi tersebut pada selang (a, b) pada sumbu x dihitung dengan rumus L = _aʃ^b (f(x) ‒ g(x)) dx.

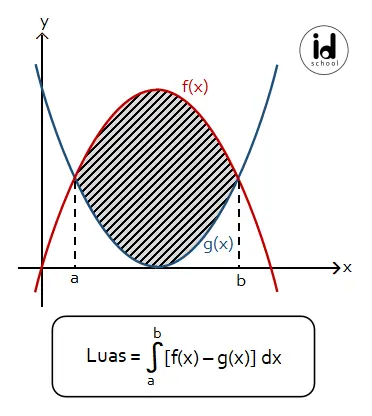
Cara menghitung luas daerah yang dibatasi oleh dua kurva ada pada penyelesaian contoh soal di bawah.

Soal:
Tentukan luas daerah yang dibatasi oleh kurva y = x² – 2x dan y = 4 – x²!

Jawab:
Pertama menentukan batas integralnya. Diperoleh dari hasil titik potong dari kedua kurva.

Menentukan batas integralnya:

x² – 2x = 4 – x²

2x² – 2x – 4 = 0

2(x² – x – 2) = 0

2(x – 2)(x + 1) = 0

Hasil: x = 2 atau x = –1

Diperoleh batas intergalnya adalah x = 2 dan x = –1. Sehingga luas daerahnya adalah L = _‒1ʃ² [(x² – 2x) – (4 ‒ x²)] dx = _‒1ʃ²  2x² – 2x ‒ 4 dx.

Menghitung luas:

Luas = _‒1ʃ²  2x² – 2x ‒ 4 dx

Sehingga,

Luas = (²/₃×2³ – 2² – 4×2) – (²/₃ × (–1³) – (–1)² – 4×(–1))

= (²/₃×8 – 4 – 8) – (–²/₃ – 1 + 4)

= ¹⁶/₃ + ²/₃ – 15 = 9 satuan luas

Jadi, luas daerah yang dibatasi oleh kurva y = x² – 2x dan y = 4 – x² adalah 9 satuan luas.

2) Batas integral pada sumbu y

Misalkan, sebuah daerah dibatasi oleh fungsi f(y) dan fungsi g(y). Luas daerah yang dibatasi oleh kedua fungsi tersebut pada selang (c, d) pada sumbu y dihitung dengan rumus L = _cʃ^d (f(y) ‒ g(y)) dy.

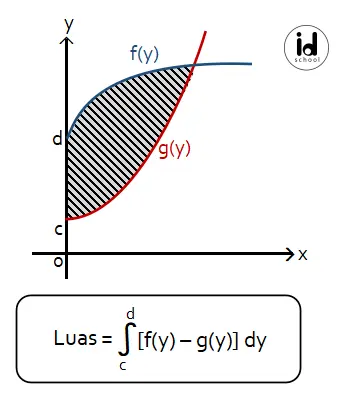
Cara menghitungnya terdapat ada pada penyelesaian soal di bawah.

Soal:
Tentukan luas daerah yang dibatasi oleh kurva x = –6y² + 4y dan x = 2 – 3y!

Jawab:
Pertama perlu untuk mengetahui batas integralnya. Batas integral diperoleh dari perpotongan dua kurva.

Menentukan batas integral:

–6y² + 4y = 2 – 3y

6y² – 3y – 4y + 2 = 0

3y(2y – 1) – 2(2y – 1) = 0

(3y – 2)(2y – 1) = 0

Hasil: y = ²/₃ dan y = ¹/₂

Batas integral untuk menghitung luasnya adalah y = ¹/₂ sampai y = ²/₃. Luas daerahnya dihitung dengan cara berikut.

Menghitung luas daerahnya:

Luas = _1/2ʃ^2/3 [(–6y² + 4y) – (2 – 3y)] dy

= _1/2ʃ^2/3 (–6y² + 7y – 2) dy

= [–2y³ + ⁷/₂y² – 2y]_¹/2^2/₃

Sehingga,

Luas = [–2(²/₃)³ + ⁷/₂(²/₃)² – 2(²/₃)] – [–2(¹/₂)³ + ⁷/₂(¹/₂)² – 2(¹/₂)]

= [–¹⁶/₂₇ + ²⁸/₁₈ – ⁴/₃)] – [–¹/₄ + ⁷/₈ – ²/₂]

= –²⁰/₅₄ + ³/₈ = –⁸⁰/₂₁₆ + ⁸¹/₂₁₆ = ¹/₂₁₆ satuan luas

Baca Juga: Rumus fungsi integral

Contoh Soal dan Pembahasan

Pembahasan soal luas daerah yang dibatasi kurva ada di bawah.

Contoh 1 – Luas daerah yang dibatasi kurva dan sumbu x

Luas daerah yang dibatasi f(x) = x² – x – 6 dan sumbu x adalah . . . satuan luas.
A. 25¹/₆
B. 20⁵/₆
C. 18²/₃
D. 16¹/₆
E. 14⁵/₆

Pembahasan:
Bentuk soal seperti ini dapat dikerjakan menggunakan cara cepat.

Mencari nilai diskriminan (D):
D = b² ‒ 4ac
D = (‒1)² ‒ 4 × 1 × (‒6) = 1 + 24 = 25

Cara menghitung luas daerah dengan cara cepat:

Jadi, luas daerah yang dibatasi f(x) = x² – x – 6 dan sumbu x adalah adalah 20⁵/₆ satuan luas.

Jawaban: B

Contoh 2 – Luas daerah yang dibatasi lebih dari satu kurva

Luas daerah yang dibatasi oleh y = ‒x² ‒ 2x; y = x² + 6x, garis x = ‒2, dan x = ‒1 adalah . . . .
A. 7⅓ satuan luas
B. 8⅓ satuan luas
C. 9⅔ satuan luas
D. 10⅔ satuan luas
E. 11⅓ satuan luas

Pembahasan:
Untuk bentuk soal ini tidak bisa dikerjakan menggunakan cara cepat. Cara mengerjakannya menggunakan rumus integral seperti langkah penyelesaian berikut.

Daerah yang dibatasi y = ‒x² ‒ 2x; y = x² + 6x, garis x = ‒2, dan x = ‒1 merupakan daerah yang diarsir berikut.

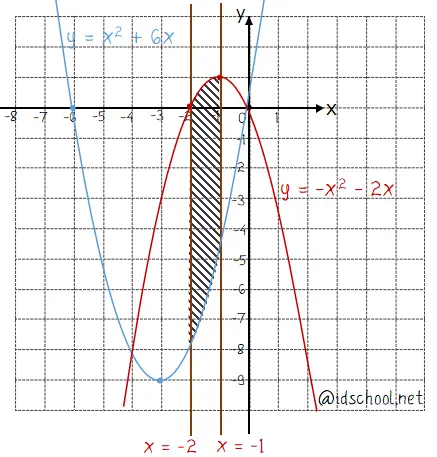
Menghitung luas daerahnya:

Luas = _–2∫^–1 [(–x² – 2x) – (x² + 6x)] dx

Luas = _–2∫^–1 (–2x² – 8x) dx = [–²/₃x³ – 4x²]_–2^–1

Sehingga,

Luas = [–²/₃(–1)³ – 4(–1)²] – [–²/₃(–2)³ – 4(–2)²]

= ²/₃ – 4 – ¹⁶/₃ + 16 = 12 – ¹⁴/₃

= 7¹/₃ sat. luas

Jadi, luas daerah yang dibatasi y = ‒x² ‒ 2x, y = x² + 6x, garis x = ‒2, dan x = ‒1 adalah 7¹/₃ satuan luas.

Jawaban: A

Contoh 3 – Menentukan rumus luas daerah yang dibatasi kurva

Perhatikan gambar di bawah!

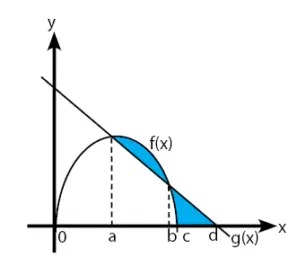
Luas daerah yang diarsir pada gambar di atas dapat dinyatakan dengan rumus . . . .

A. _a∫^b (f(x) – g(x)) dx + _b∫^d g(x) dx – _b∫^c f(x) dx

B. _a∫^b (f(x) – g(x)) dx + _b∫^d (g(x) dx – f(x)) dx

C. _a∫^d (f(x) – g(x)) dx

D. _a∫^d (f(x) – g(x)) dx – _c∫^d g(x) dx

E. _a∫^b (f(x) – g(x)) dx + _c∫^d (g(x) – f(x)) dx

Pembahasan:
Untuk mendapatkan luas daerah yang dibatasi kurva, dapat diperoleh dengan membagi luas daerah menjadi beberapa bagian.

Perhatikan gambar di bawah.

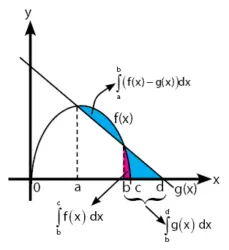
Jadi, persamaan untuk menghitung luas daerah yang diarsir adalah Luas = _aʃ^b (f(x) ‒ g(x)) dx + ʃ_b^d g(x) dx ‒  ʃ_b^c f(x) dx.

Jawaban: A

Sekian bahsan rumus luas daerah yang dibatasi kurva dan contoh cara menghitungnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Rumus Volume Benda Putar