Definisi Turunan Fungsi dan 8 Teorema + Pembuktiannya

Sebuah fungsi f(x) memiliki fungsi turunan pertamanya adalah f'(x), jika nilai limitnya ada. Sebagai contoh fungsi yang selalu memiliki nilai limit yaitu fungsi linear, misalkan f(x) = 3x + 6. Turunan pertama dari f(x) = 3x + 6 adalah f'(x) = 3.

Hasil turunan fungsi linear f(x) biasanya mudah untuk dicari. Seperti pada contoh fungsi f(x) = 3x + 6. Namun untuk fungsi yang kompleks membutuhkan teknik pengerjaan.

Lebih banyak mengenai turunan fungsi terdapat pada teorama turunan fungsi di bawah.

Daftar isi:

• Definisi Turunan Fungsi
• 8 Teorema Turunan Fungsi
  • Teorema 1 – Turunan Konstanta
  • Teorema 2 (Turunan Fungsi Identitas)
  • Teorema 3 (Aturan Pangkat)
  • Teorema 4 (Aturan Kelipatan Konstanta)
  • Teorema 5 (Aturan Jumlah)
  • Teorema 6 (Aturan Selisih)
  • Teorema 7 (Aturan Turunan Hasil Kali Fungsi)
  • Teorema 8 (Aturan Hasil Bagi)

Definisi Turunan Fungsi

Fungsi turunan menyatakan laju perubahan suatu variabel terhadap variabel lain. Teori mengenai turunan fungsi diawali oleh sebuah permasalahan gradien garis singgung oleh ilmuwan besar Yunani, Archimedes (287 s.d. 212 SM).

Sebuah kurva y = f(x) memuat dua titik P dan Q dengan koordinat masing-masing adalah P(c, f(c)) dan Q(c+h, f(c+h)). Kemiringan garis PQ dapat ditentukan melalui persamaan tangen.

Baca Juga: Rumus Turunan Fungsi Trigonometri

Euclid mengungkapkan gagasannya tentang garis singgung yang menyentuh kurva pada satu titik. Gagasan tersebut berfungsi untuk persamaan lingkaran tetapi tidak berfungsi pada beberapa kurva.

Diperoleh hasil turunan fungsi f(x) pada definisi turunan seperti berikut.

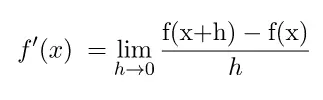
Contoh cara mendapatkan hasil turunan f(x) menggunakan definisi turunan terdapat pada langkah penyelesaian di bawah.

Soal:
Tentukan turunan pertama dari persamaan f(x) = 13x + 8 menggunakan definisi turunan!

Penyelesaian:

Diketahui f(x) = 13x + 8,

maka f(x + h) = 13(x + h) + 8 = 13x + 13h + 8

Menentukan f'(x) menggunakan difinisi turunan:

Diperoleh hasil turunan pertama f(x) = 13x + 8 menggunakan definisi turunan adalah f'(x) = 13.

Baca Juga: Interval Fungsi Naik dan Turun

Cara mendapatkan f'(x) menggunakan definisi turunan seperti yang dilakukan di atas membutuhkan waktu lama dan tidak efisien. Untuk cara yang lebih cepat dan gampang, sobat idschool dapat memanfaat teorema-teorema yang berlaku pada turunan.

8 Teorema Turunan Fungsi

Setidaknya ada delapan teorema yang dapat digunakan untuk menentukan hasil turunan suatu fungsi. Kedelapan teorema turunan beserta buktinya diberikan pada detail di bawah.

Teorema 1 – Turunan Konstanta

Turunan dari sebuah konstanta f(x) = k adalah f'(x) = 0, k = konstanta.

Bukti:

Diketahui fungsi f(x) = k

Maka,

Contoh penggunaan Teorema 1 untuk menentukan hasil turunan pertama suatu fungsi terapat pada penyelesaian soal berikut.

Soal:
Tentukan turunan pertama dari fungsi f(x) = 7!

Jawab:

Diketahui f(x) = 7

Maka f'(x) = 0

Jadi, turunan pertama f(x) = 7 adalah f'(x) = 0.

Teorema 2 (Turunan Fungsi Identitas)

Jika f(x) = x maka f'(x) = 1

Bukti:

Diketahui f(x) = x

Sehingga f(x + h) = x + h

Contoh penggunaan Teorema 2 digunakan untuk menetukan hasil turunan fungsi pada soal berikut.

Soal:
Tentukan turunan pertama dari fungsi f(x) = 7x!

Jawab:

Diketahui f(x) = 7x

Maka,

f'(x) = 7 · 1 = 7

Jadi, turunan pertama f(x) = 7x adalah f'(x) = 7.

Baca Juga: Cara Menentukan Nilai Maksimum/Minimum dari Fungsi Trgonometri

Teorema 3 (Aturan Pangkat)

Jika f(x) = xⁿ maka f'(x) = n ⋅ xⁿ⁻¹ dengan n merupakan bilangan bulat positif.

Atau secara matematis dapat juga dituliskan dengan persamaan: D(xⁿ) =n⋅ x^n-1 dx.

Bukti:
Langkah pembuktian teorema 3 mengenai aturan pangkat terdapat pada cara berikut.

Contoh penggunaan Teorema 3 untuk menentukan hasil turunan pertama terdapat pada soal di bawah.

Soal:
Tentukan hasil turunan pertama fungsi f(x) = x⁹!

Jawab:

D_x(x⁹) = 9x^9-1 + C

D_x(x⁹) = 9x⁸ + C

Jadi, turunan pertama f(x) = x⁹ adalah f'(x) = 9x⁸.

Teorema 4 (Aturan Kelipatan Konstanta)

Jika k dan f berturut-turut adalah konstanta dan suatu fungsi yang dapat diturunkan, maka (kf)'(x) = k ⋅ f'(x) atau dinotasikan dengan persamaan berikut.

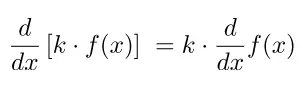
Bukti:
Andaikan F(x) = k⋅f(x) maka akan diperoleh persamaan F'(x) seperti berikut.

Contoh penggunaan Teorema 4 untuk menyelesaikan hasil turunan pertama terdapat pada penyelesaian soal di bawah.

Soal:
Tentukan turunan pertama dari f(x) = -5x⁴!

Jawab:

D_x(-5x⁴ ) = -5 ⋅ D_x(x⁴)

= -5 ⋅ (4x³)

= -20x³

Jadi, turunan pertama dari f(x) = -5x⁴ adalah f'(x) = -20x³

Teorema 5 (Aturan Jumlah)

Jika f dan g adalah fungsi-fungsi yang dapat diturunkan, maka (f + g)'(x) = f'(x) + g'(x) atau dinotasikan dengan persamaan berikut.

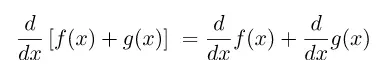
Bukti:
Andaikan F(x) = f(x) + g(x) maka:

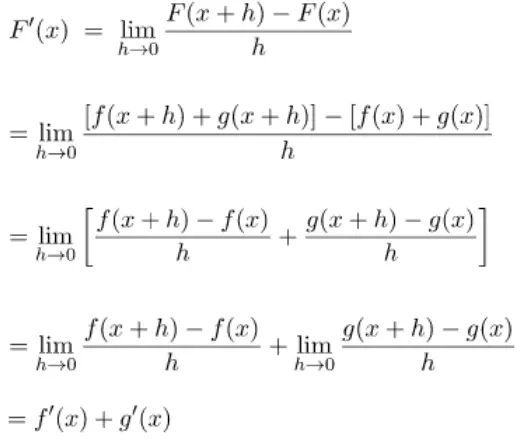
Contoh penggunaan Teorema 5 untuk menentukan hasil turunan pertama terdapat pada langkah penyelesaian di bawah.

Soal:
Tentukan turunan pertama dari f(x) = 5x⁴ + 8x!

Jawab:

D_x( 5x⁴ + 8x) = D_x(5x⁴) + D_x(8x)

= 5 ⋅ D_x(x⁴) + 8 ⋅ D_x(x)

= 5 ⋅ 4x³ + 8 ⋅ 1 = 20x³ + 8

Jadi, hasil turunan pertama dari f(x) = 5x⁴ + 8x adalah f'(x) = 20x³ + 8.

Baca Juga: Tips Cara Menyelesaikan Limit Fungsi

Teorema 6 (Aturan Selisih)

Jika f dan g adalah fungsi-fungsi yang dapat diturunkan, maka (f – g)'(x) = f'(x) – g'(x) atau dinotasikan dengan persamaan berikut.

Bukti:
Andaikan F(x) = f(x) – g(x) maka turunan fungsi F(x) atau F'(x) akan memenuhi persamaan berikut.

Contoh Penggunaan Teorema 6 digunakan untuk menentukan hasil turunan fungsi pada soal berikut.

Soal:
Tentukan turunan pertama dari f(x) = 6x − 2x³!

Jawab:

D_x(6x − 2x³) = D_x(6x) − D_x(2x³)

= 6 ⋅ D_x(x) − 2 ⋅ D_x(x³)

= 6 ⋅ 1 − 2 ⋅ 3x² = 6 − 6x²

Jadi, hasil turunan pertama f(x) = 6x − 2x³ adalah f'(x) = 6 − 6x².

Teorema 7 (Aturan Turunan Hasil Kali Fungsi)

Jika f dan g adalah fungsi-fungsi yang dapat diturunkan, maka (f × g)'(x) = f(x)g'(x) + g(x)f'(x) atau dapat dinotasikan dengan persamaan berikut.

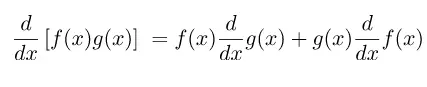
Bentuk arutan hasil kali sering dinyatakan dalam persamaan u dan v, misalkan u = f(x) dan v = g(x) maka: D_x(uv) = u⋅D_x(v) + v⋅D_x(u) = uv’ + vu’.

Bukti:
Andaikan F(x) = f(x) × g(x) maka turunan fungsi hasil kali akan memenuhi persamaan berikut.

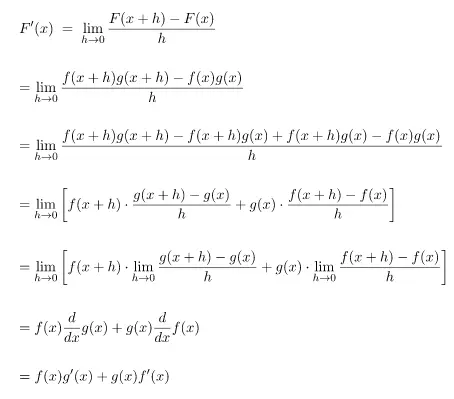
Contoh penggunaan Teorema 7 untuk menentukan hasil turunan pertama terdapat pada langkah penyelesaian soal di bawah.

Soal:
Jika diketahui: f(x) = (3x² − 2)(5x − 4) maka f'(x) = ….

A. 45x² − 24x − 10

B. −45x² − 24x − 10

C. 45x² + 24x − 10

D. 45x² − 24x + 10

E. −45x² − 24x + 10

Jawab:
Hasil turunan f(x) dari persamaan di atas dapat diselesaikan menggunakan rumus: f(x) = u ⋅ v → f'(x) = u’ ⋅ v + u⋅v’.

Misal:
u = 3x² − 2
u’ = D_x(3x² − 2) = 6x

v = 5x−4
v’ = D_x(5x − 4) = 5

Sehingga,

f'(x) = 6x(5x − 4) + 5(3x² − 2)

=30x² − 24x + 15x² − 10

=45x² − 24x − 10 (A)

Teorema 8 (Aturan Hasil Bagi)

Jika f dan g adalah fungsi-fungsi yang dapat diturunkan, dengan g(x) ≠ 0 maka

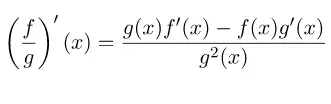
Misalkan u = f(x) dan v = g(x) maka:

Bukti:
Andaikan F(x) = ^f(x)/_g(x) maka turunan fungsi F(x) akan memenuhi persamaan di bawah.

Contoh penggunaan Teorema 8 untuk menentukan hasil turunan fungsi terdapa pada soal dan pembahasan di bawah.

Soal:

Jawab:

Misakan:

u = 2x − 3 → u’ = D_x(2x − 3) = 2

v = x³ + 5 → v’ = D_x(x³ + 5) = 3x²

Sehingga turunan pertama f(x) dapat dicari dengan cara berikut.

Demikianlah tadi ulasan pengertian dan definisi turunan fungsi, terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!