Pengantar materi vektor SMA antara lain meliputi notasi vektor, panjang vektor, operasi hitung antar dua vektor, sudut antara dua vektor, dan proyeksi vektor. Vektor merupakan salah satu jenis besaran vektor dari dua jenis besaran yang ada (besaran skalar dan besaran vektor). Besaran vektor adalah jenis besaran yang memiliki nila) dan arah, contohnya adalah kecepatan, momentum, gaya, dan lain sebagainya.
Vektor digambarkan sebagai ruas garis yang memiliki keterangan besar dan penunjuka panah sebagai arah. Letak vektor di ruang dimensi dua (R2) didefinisikan sebagai pasangan berurutan dua buah bilangan real (x, y) atau dalam bentuk matrik 2×1. Sedangkan pada ruang dimensi tiga (R3) dinyatakan dalam sebuah urutan bilangan real (x, y, z) atau bentuk matriks dengan ukuran 3×1. Simbol vektor dinyatakan dalam huruf kecil yang diberi tanda anak panah di atasnya. Selain itu vektor juga dapat disimbolkan dengan huruf kecil yang dicetak tebal atau huruf kecil dengan ruas garis di atasnya.

Dari gambar di atas, titik A disebut titik pangkal (titik tangkap atau titik asal) dan titik B disebut titik ujung (terminal) dari vektor a. Panjang vektor a adalah panjang ruas garis AB yang dinyatakan dalam simbol | a | = | AB |.
Table of Contents
- Vektor pada Ruang Dimensi Dua (R2)
- Vektor di Ruang Dimensi 3 (R3)
- Contoh Soal Pengantar Materi Vektor + Bahas
Vektor pada Ruang Dimensi Dua (R2)
Pengantar materi vektor pertama adalah vektor yang berada di ruang dimensi dua. Ruang dimensi dua merupakan bidang datar yang memiliki dua sumbu yaitu sumbu x dan sumbu y. Jadi, vektor yang berada pada ruang dimensi dua memiliki dua faktor penentu arah yaitu sumbu x dan sumbu y.
Cara menyatakan vektor pada ruang dimensi dua berupa susunan bilangan real, di mana urutan pertama merupakan arah untuk absis (sumbu-x) dan urutan kedua merupakan arah untuk ordinat (sumbu-y).
Penulisan vektor juga dapat menggunakan keterangan simbol vektor satuan. Simbol penulisan vektor satu satuan pada ruang dimensi dua di sumbu x positif adalah i. Sedangkan simbol penulisan vektor satu satuan pada ruang dimensi dua di sumbu y positif adalah j. Contoh vektor dengan persamaan vektor v = 3i + 5j artinya berada di absis x = 3 dan ordinat y = 5.
Selanjutnya, perhatikan gambar contoh vektor-vektor berikut.
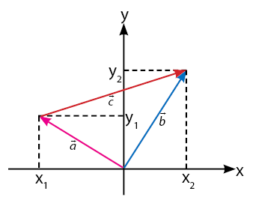
Keterangan:
a = (x1, y1)
b = (x2, y2)
c = (x2 ‒ x1, y2 ‒ y1)
Sebuah vektor dapat ditentukan panjangnya berdasarkan keterangan pada arah vektor. Jika sebuah vektor disimbolkan dengan a maka panjang vektor dinotasikan dengan | a |. Rumus panjang vektor a, b, dan c adalah sebagai berikut.

Baca Juga: Besar Sudut Antara Vektor a dan b
Vektor di Ruang Dimensi 3 (R3)
Pembahasan materi vektor selanjutnya adalah vektor di Ruang Dimensi tiga (R3). Arah vektor pada ruang dimensi tiga ditentukan oleh tiga faktor penentu arah, yaitu sumbu-x, sumbu y, dan sumbu-z. Cara menyatakan vektor pada ruang dimensi tiga berupa susunan bilangan real, di mana urutan pertama merupakan arah untuk sumbu-x, urutan ke dua untuk arah untuk sumbu-y, dan urutan ke tiga untuk arah sumbu-z.
Vektor-vektor satuan pada sumbu x positif, y positif, dan z positif dapat juga disimbolkan dengan huruf i, j, dan k yang sesuai dengan persamaan matriks berikut.
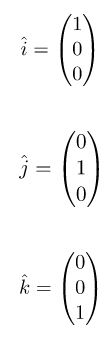
Selanjutnya, perhatikan gambar vektor pada ruang dimensi tiga di bawah!

Vektor pada ruang dimensi tiga juga dapat diketahui panjangnya melalui koordinat arah pada simbol vektor. Jika P(x, y, z) adalah sembarang titik di ruang dimensi tiga, maka panjang vektor tersebut dapat dihitung melalui rumus berikut.

Baca Juga: Penjumlahan dan Pengaturan Vektor Serta Sifat-sifatnya
Contoh Soal Pengantar Materi Vektor + Bahas
Perhatikan gambar balok berikut!
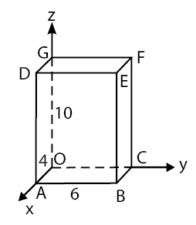
Balok ABCO-DEFG memiliki ukuran | OA | = 4, | AB | = 6, dan | OG | = 10. Nilai cosinus sudut antara vektor OA dan AC adalah ….
A. ‒8/3√13
B. ‒3/2√13
C. ‒8/13√13
D. 8/√13
E. 13/√13
Pembahasan:
Berdasarkan gambar dan keterangan pada soal dapat diperoleh informasi letak koordinat O(0, 0, 0), A (4, 0, 0), B(4, 6, 0), C(0, 6, 0), D(4, 0, 10), E(4, 6, 10), F(0, 6, 10), dan G(0, 0, 10).
Perhatikan letak sudut α pada gambar di bawah.

Menentukan letak koordinat vektor OA, AC:
OA = (4, 0, 0) – (0, 0, 0) = (4, 0, 0)
AC = (0, 6, 0) – (4, 0, 0) = (-4, 6, 0)
Menentukan panjang vektor AC:
| AC |2 = (‒4)2 + 62 + 02
| AC |2 = 16 + 36 + 0 = 52
| AC | = √52
| AC | = √(4 × 13)
| AC | = 2√13
Menentukan nilai cosinus antara vektor OA dan AC:

Jawaban: C
Demikianlah tadi pengantar materi vektor di tingkat Sekolah Menengah Atas. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Perbandingan Vektor pada Sebuah Ruas Garis
