Pelaksanaan TKA untuk jenjang SMA/MA/SMK/MAK/Sederajat dijadwalkan berlangsung pada bulan November 2025. Melalui halaman Simulasi TKA, Kementerian Pendidikan Dasar dan Menengah (Kemendikdasmen) memberikan beberapa contoh soal TKA, tanpa pembahasan. Pembahasan contoh soal TKA Matematika Tahun 2025 untuk jenjang SMA diulas dl di bawah.
Daftar isi:
Contoh 1
Pada trapesium berikut, AD = BC, AB sejajar DC, AB > DC, ∠BAD = 70o, dan ∠ABD = 30o.
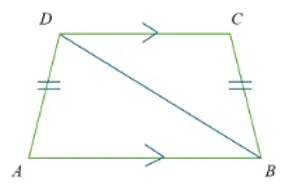
Tentukan Benar atau Salah untuk setiap pernyataan berikut terkait dengan besar sudut pada trapesium ABCD!
| Pernyataan | Benar | Salah |
| ∠BCD = 110o | √ | |
| ∠CBD = 40o | √ | |
| ∠BDC = 40o | √ |
Pembahasan:
Untuk mengetahui mengerjakan soal ini, sobat idschool perlu mengetahui sifat sudut pada trapesium.
Sifat sudut pada trapesium adalah memiliki jumlah sudut 180o untuk sepasang sudut pada sisi sejajar. Pada trapesium sama kaki, sudut-sudut yang ada di sepanjang sisi sejajar memiliki besar yang sama.
Sehingga dapat disimpulkan bahwa,
besar ∠BAD = ∠ABC
besar ∠BAD + ∠ADC = 180o dan besar ∠ABC + ∠BCD = 180o
Diketahui besar ∠BAD = 70o dan ∠ABD = 30o, maka:
Besar ∠BCD = 180o – besar ∠ABC
= 180o – besar ∠ABC
= 180o – 70o = 110o
[Pernyataan (1) Benar]
Besar ∠CBD = ∠ABC – ∠ABD
= ∠BAD – 30o
= 70o – 30o = 40o
[Pernyataan (2) Benar]
Pernyataan selanjutnya,
Besar ∠BDC = ∠ADC – ∠ADB
= ∠BCD – 30o
= 110o – 30o = 80o
[Pernyataan (3) Benar]
Contoh 2
Seorang murid memperkirakan banyaknya penonton suatu video dalam ribuan yang dibuat oleh content creator A di media sosial mengikuti model f(t) = 3(2t) dengan t adalah banyaknya hari sejak video diunggah.
Tentukan Benar atau Salah untuk setiap pernyataan berikut!
| Pernyataan | Benar | Salah |
| Video tersebut hanya ditonton oleh 3.000 penonton setelah tepat 24 jam diunggah. | √ | |
| Banyaknya penonton video meningkat dua kali lipat dari hari sebelumnya untuk beberapa hari setelah diunggah. | √ | |
| Model banyaknya penonton ini tidak tepat untuk waktu yang cukup besar. | √ |
Pembahasan:
Fungsi banyak penonton video: f(t) = 3(2t) = 3 × 2t, dengan t adalah banyaknya hari sejak video diunggah.
Untuk t = 24 jam = 1 hari,
Sehingga f(1) = 3(2) = 3 × 2 = 6 penonton. Pernyataan (1) Benar.
Saat t = 1 → f(1) = 6
Untuk t = 2 → f(2) = 3(4) = 3 × 4 = 12
Untuk t = 3 → f(3) = 3(6) = 3 × 6 = 18
Banyak penononton pada hari ke-3 bukan kelipatan dari hari sebelumnya. Jadi, pernyataan (2) Salah.
Fungsi banyak penonton f(t) = 3(2t) merupakan fungsi linear, model bisa digunakan untuk berapapun banyak penontonnya. Jadi, pernyataan (3) Salah.
Contoh 3
Pembahasan:
Operasi perkalian didahululan dari operasi penjumlahan.
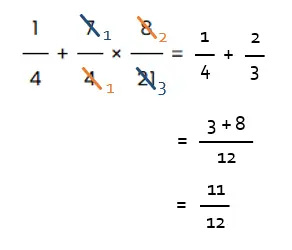
Jadi, jawabannya adalah C.
Baca Juga: Operasi Hitung Pecahan
Contoh 4
Mirna akan memproduksi dua jenis kue dengan modal Rp8.000.000,00. Biaya produksi kue bolu sebesar Rp15.000,00 per kotak dan dijual dengan laba 40%. Sedangkan biaya produksi kue brownies sebesar Rp20.000,00 per kotak dan dijual dengan laba 35%. Setiap harinya, Mirna dapat memproduksi paling banyak 500 kotak kue.
Apabila Mirna ingin memperoleh keuntungan maksimum, tentukan Benar atau Salah untuk setiap pernyataan berikut!
| Pernyataan | Benar | Salah |
| Mirna harus memproduksi 200 kotak kue bolu. | ||
| Mirna harus memproduksi kue brownies lebih banyak. | ||
| Keuntungan maksimum yang dapat diperoleh Mirna adalah Rp3.100.000,00. |
Pembahasan:
Dari soal diketahui beberapa informasi berikut.
- Modal Mirna Rp8.000.000,00
- Biaya produksi kue bolu = Rp15.000,00 per kotak
- Harga jual kue bolu (untung 40%)
= 140/100 × 15.000
= 21.000
- Biaya produksi kue brownies = Rp20.000,00 per kotak
- Harga jual kue brownies (untuk 35%)
= 135/100 × 20.000
= 27.000 - Banyak produksi = 500 kotak kue per hari
Soal ini merupakan masalah program linear. Misalkan banyak produksi kue bolu = B dan banyak produksi kue brownies = R, maka soal cerita dapat menghasilkan pertidaksamaan berikut.
Pernyataan (i):
15.000B + 20.000R ≤ 8.000.000
3B + 4R ≤ 1.600
Pernyataan (ii):
B + R ≤ 500
Fungsi tujuan: memaksimalkan Z = 21.000B + 27.000R
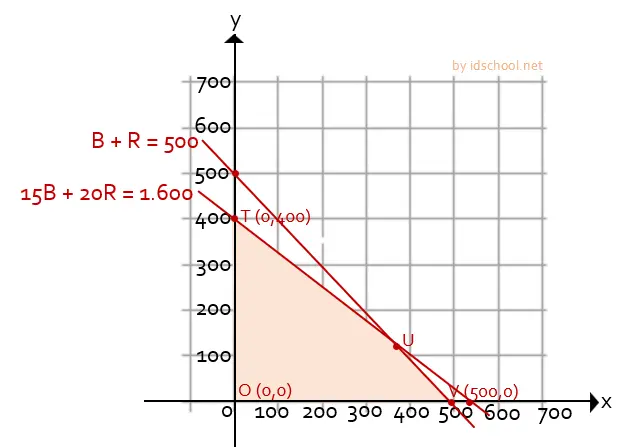
Menentukan nilai B dan R agar mengahsilkan fungsi Z maksimum dengan metode titik pojok.
Diperoleh titik pojok T, U, dan V dengan koordinat T(0, 400) dan V(500, 0). Sementara titik pojok U belum diketahui. Untuk itu perlu dicari terlebih dahulu.
Diketahui,
B + R = 500
B = 500 – R
Sehingga,
3B + 4R = 1.600
3(500 – R) + 4R = 1.600
1.500 – 3R + 4R = 1.600
R = 1.600 – 1.500
R = 100
Nilai B = 500 – R = 500 – 100 = 400, maka koordinat U(400, 100)
Keuntungan yang diperoleh pada setiap titik pojok:
| Koordinat | Keuntungan maksimum |
| T(0, 400) | Z = 0 × 21.000 + 400 × 27.000 Z = 0 + 10.800.000 = 10.800.000 |
| U(400, 100) | Z = 400 × 21.000 + 100 × 27.000 Z = 8.400.000 + 2.700.000 = 11.100.000 (maksimal) |
| V(500, 0) | Z = 500 × 21.000 + 0 × 27.000 Z = 10.500.000 + 0 = 10.500.000 |
Dengan metode titik pojok diperoleh penghasilan maksimal ketika produksi bolu sebanyak B = 400 dan brownies sebanyak R = 100.
Sehingga,
i) Produksi kue bolu = 400 → Pernyataan (1) SALAH
ii) Produksi kue brownies = 100, lebih sedikit dari produksi kue bolu → Pernyataan (2) SALAH
iii) Penghasilan maksimal yang diperoleh adalah 11.100.000, sehingga keuntungan maksimal = 11.100.000 – 8.000.000 = Rp3.100.00,00 → Pernyataan (3) BENAR
Contoh 5
Pada trapezium siku-siku tersebut, AB= 3 dan AD <= BC. Apakah keliling trapesium tersebut lebih dari 25?
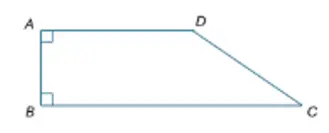
Putuskan apakah dengan tambahan informasi Pernyataan (1) dan Pernyataan (2) berikut cukup untuk menjawab pertanyaan tersebut!
(1) Luas trapesium ABCD = 24.
(2) BC = 10 dan CD = 5.
A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi Pernyataan (2) SAJA tidak cukup.
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi Pernyataan (1) SAJA tidak cukup.
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan Pernyataan (2) SAJA cukup.
E. Pernyataan (1) dan Pernyataan (2) tidak cukup untuk menjawab pertanyaan.
Contoh 6
Rata-rata nilai ulangan 17 murid dari skala 100 adalah 83. Ada 3 murid yang mengikuti ujian susulan sehingga rata-rata nilai ulangan dari 20 murid menjadi 82.
Tentukan semua pernyataan berikut yang benar terkait dengan nilai ketiga murid yang mengikuti ujian susulan! Jawaban benar lebih dari satu.
- Jumlah nilai ketiga murid yang mengikuti ujian susulan adalah 229.
- Rata-rata nilai ketiga murid yang mengikuti ujian susun lebih dari 70.
- Nilai terendah dari ketiga murid yang mengikuti ujian susulan tidak kurang dari 29.
- Nilai tertinggi dari ketiga murid yang mengikuti ujian susulan lebih dari 76.
- Jangkauan data nilai ketiga murid yang mengikuti ujian susulan lebih dari 72.
Pembahasan:
Demikianlah tadi pembahasan contoh soal TKA Matematika untuk tingkat SMA/MA/SMK/MK/Sederajat tahun 2025. Terima kasih atas kunjungannya!
