Dua buah pecahan atau lebih dapat dilakukan suatu operasi hitung yang meliputi penjumlahan, pengurangan, perkalian, atau pembagian. Cara melakukan operasi hitung pecahan pada penjumlahan dan pengurangan hanya bisa dilakukan pada pecahan dengan penyebut sama. Sedangkan operasi hitung pecahan pada perkalian dan pembagian dapat dilakukan pada bentuk pecahan biasa dengan penyebut sama atau berbeda.
Bilangan bentuk pecahan ditulis dengan dua buah bilangan bulat yang disusun atas bawah dan dipisahkan sebuah garis lurus. Bagian atas garis merupakan pembilang sedangkan bagian bawah merupakan penyebut. Secara umum, penulisan pecahan biasa dinyatakan dalam bentuk a⁄b. Contoh bilangan pecahan ¾, nilai pembilang = 3 dan nilai penyebut = 4.
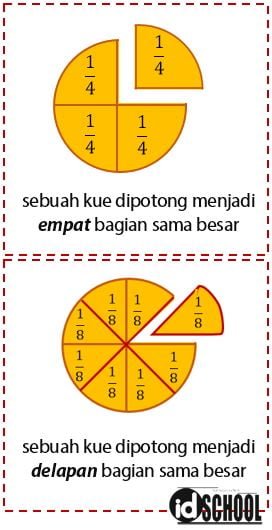
Pecahan menyatakan bagian-bagian dari sebuah benda yang utuh. Sebagai contoh, misalkan sobat idschool mempunyai sebuah kue. Kemudian, Ibu membagi kue tersebut menjadi empat bagian sama panjang. Masing-masing bagian kue tersebut menjadi satu per empat bagian. Penulisan notasi bilangan satu per empat sama dengan ¼.
Jika Ibu memotong kue menjadi delapan bagian sama panjang maka masing-masing bagian akan menjadi lebih kecil. Setiap bagian kue yang dipotong menjadi delapan bagian sama besar dinyatakan dalam pecahan 1⁄8.
Baca Juga: Operasi Hitung Campuran Negatif-Positif
Bagaimana cara melakukan operasi hitung pecahan? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Macam – Macam Pecahan
- Cara Melakukan Operasi Hitung Pecahan
- Contoh Soal Operasi Hitung Pecahan dan Pembahasan
Macam – Macam Pecahan
Ada empat macam pecahan yang biasa digunakan sehari-hari. Keempat macam pecahan tersebut meliputi pecahan biasa, campuran, desimal, dan bentuk persen. Kenali bentuk empat macam pecahan pada masing-masing ulasan di bawah.
1) Pecahan Biasa
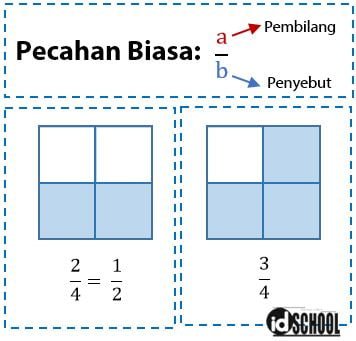
Bentuk pecahan biasa diberikan dalam bentuk a⁄b, yaitu dua bilangan bulat yang dipisahkan sebuah garis lurus. Bilangan pada posisi atas disebut pembilang. Sedangkan yang berada pada posisi bawah disebut penyebut. Contoh pecahan biasa adalah ½, ¾, ¼, dan lain sebagainya.
2) Pecahan Campuran
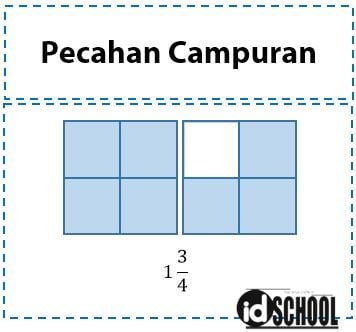
Pecahan campuran merupakan gabungan bilangan bulat dengan pecahan biasa. Bilangan bulat pada pecahan campuran berada sebelum pecahan biasa. Contoh campuran adalah 1½, 2¾, 3⁵⁄₈, dan lain sebagainya.
3) Pecahan Desimal
Karakteristik pecahan desimal adalah penggunaan tanda koma setelah bilangan bulat pertama. Banyaknya angka setelah tanda koma dapat berjumlah satu, dua, tiga, bahkan sampai tak hingga. Dalam pecahan biasa, nilai pecahan desimal adalah pecahan yang mempunyai penyebut khusus yaitu sepuluh, seratus, seribu, dan seterusnya. Contoh pecahan desimal seperti 0,6; 0,75, dan lain sebagainnya.

4) Persen dan Permil
Berikutnya adalah pecahan dalam bentuk persen dan permil. Ciri khas dari pecahan dengan bentuk persen adalah adanya tanda % (persen) dan ‰ (permil). Nilai persen (%) sama dengan per seratus, sedangkan permil (‰) sama dengan per seribu. Tanda % atau ‰ mengikuti setelah bilangan bulat. Contoh pecahan dengan persen dan permil adalah 1%, 35%, 125‰, dan lain sebagainya.

Baca Juga: Rumus Persentase Untung dan Rugi
Cara Melakukan Operasi Hitung Pecahan
Aturan pengerjaan operasi hitung pecahan sama seperti pada operasi hitung bilangan bulat. Urutan pengerjaan dilakukan dari pangkat/akar, tanda kurung, perkalian/pembagian, kemudian penjumlahan/pengurangan. Pengerjaan untuk derajat operator yang sama (misalnya penjumlahan dengan pengurangan atau perkalian dengan pembagian) dilakukan dari kiri ke kanan.
Selain perlu memperhatikan aturan operasi hitung pada bilangan bulat, ada hal lain yang perlu diperhatikan. Beberapa langkah yang perlu diperhatikan dalam operasi hitung pecahan diberikan seperti berikut.
1) Penjumlahan Pecahan
Penjumlahan tidak dilakukan antar pembilang dan penyebut. Namun, dua buah pecahan dapat dijumlah jika memiliki nilai penyebut yang sama. Jika penyebut pada dua buah pecahan atau lebih tersebut belum sama maka perlu disamakan terlebih dahulu. Penyebut dapat disamakan dengan cara mengubahnya dalam nilai KPK dari kedua bilangan yang menjadi penyebut.
Perhatikan contoh cara melakukan penjumlah pecahan berikut.
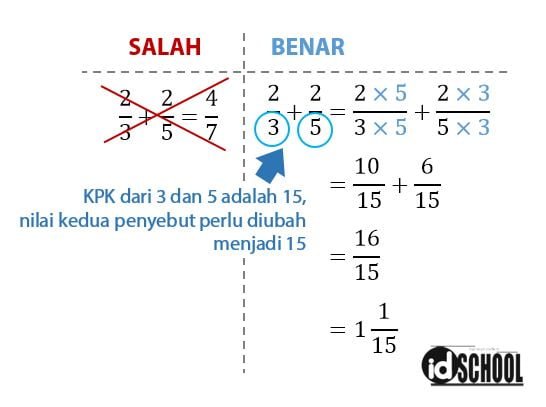
Baca Juga: Cara Cepat Mencari KPK dan FPB
2) Pengurangan Pecahan
Operasi hitung pecahan pada pengurangan dapat dilakukan dengan menyamakan penyebutnya terlebih dahulu. Cara melakukan operasi hitung pengurangan pecahan sama seperti pada penjumlahan. Perhatikan cara mengerjakan operasi hitung pengurangan pecahan berikut.
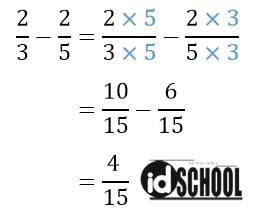
3) Perkalian Pecahan
Operasi hitung pecahan berikutnya adalah perkalian pecahan. Pada perkalian pecahan, sobat idschool tidak perlu menyamakan penyebutnya terlebih dahulu. Perkalian pecahan dilakukan antar pembilang dengan pembilang dan penyebut dengan penyebut.
Perhatikan contoh operasi hitung pecahan pada perkalian pecahan berikut.

4) Pembagian Pecahan
Terakhir adalah operasi hitung pembagian pada pecahan. Untuk melakukan pembagian pecahan cara yang dilakukan adalah membalik pecahan pada posisi akhir dan merubah tanda menjadi kali.
Selanjutnya operasi hitung yang dilakukan sama seperti pada perkalian. Di mana caranya adalah dengan mengalikan antara pembilang dengan pembilang dan penyebut dengan penyebut. Atau, operasi hitung pembagian pecahan dilakukan dengan mengalikan pembilang pecahan pertama dengan penyebut pecahan kedua dan penyebut pertama dengan pembilang kedua.
Lebih lengkapnya simak penyelesaian pembagian pecahan pada contoh di bawah.
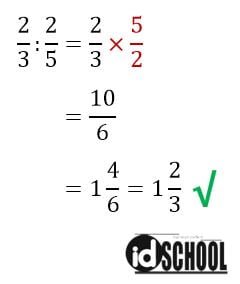
Baca Juga: Operasi Hitung Campuran Bilangan Bulat
Contoh Soal Operasi Hitung Pecahan dan Pembahasan
Berikut ini adalah soal-soal dengan materi operasi hitung pecahan. Bahasan contoh soal meliputi soal mengurutkan pecahan, operasi hitung pecahan, dan soal cerita tentag pecahan. Contoh soal juga telah dilengkapi dengan pembahasan untuk menambah pemahaman sobat idschool. Selamat Berlatih!
Contoh 1 – Soal Mengurutkan Pecahan

Pembahasan:
Dengan bentuk pecahan seperti pada soal tentu tidak mudah untuk mengurutkan pecahan. Agar dapat mengurutkan nilai pecahan perlu menyamakannya kedalam satu jenis yang sama terlebih dahulu.
Semua bentuk pecahan perlu diubah kedalam bentuk yang sama kemudian diurutkan. Bentuk pecahan dapat dipilih sesuai kesukaan masing-masing.
Misalnya pada pembahasan kali ini akan diubah bentuk pecahan ke dalam pecahan biasa. Kemudian dari bentuk pecahan biasa selanjutnya dapat dengan mudah untuk diurutkan.

Jawaban: D
Baca Juga: Cara Mencari Akar Pangkat Tiga dari Suatu Bilangan
Contoh 2 – Operasi Hitung Pecahan

Pembahasan:
Dalam soal ada pembagian, sehingga perhitungannya perlu dilakukan terlebih dahulu.

Jawaban: D
Contoh 3 – Soal Cerita Tentang Pecahan
Ibu memiliki persediaan beras sebanyak 50 kg. Setiap hari ibu memakai beras sebanyak ⁵⁄₈ kg. Beras persediaan Ibu akan habis digunakan dalam waktu … hari.
A. 32
B. 24
C. 16
D. 8
Pembahasan:
Cara menghitung lama waktu sampai beras persediaan ibu habis adalah melakukan operasi hitung untuk jumlah beras dibagi banyak beras yang dipakai setiap harinya.
Menghitung beras persediaan ibu akan habis dalam waktu:

Jawaban: C
Demikianlah tadi ulasan materi operasi hitung pecahan yang meliputi berbagai bentuk pecahan dan cara melakukan operasi hitung pecahan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Rumus Keliling dan Luas Lingkaran