Pembuktian rumus sinus jumlah dua sudut sin (A+B) dan sin (A-B )

Rumus sinus jumlah dua sudut memiliki bentuk identitas sin (A+B) = sin A ∙ cos B + cos A ∙ sin B. Sedangkan rumus sinus selisih dua sudut memiliki bentuk identitas sin (A−B) = sin A ∙ cos B − cos A ∙ sin B. Pembuktian rumus sin (A+B) dan sin (A−B) dapat menggunakan identitas trigonometri untuk rumus cosinus jumlah dan selisih dua sudut, sin (90^o−A) = cos A, dan cos (90^o−A) = sin A.

Bagaimana pembuktian rumus sin (A+B) = sin A ∙ cos B + cos A ∙ sin B? Bagaimana pembuktian rumus sin (A−B) = sin A ∙ cos B − cos A ∙ sin B? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Pembuktian rumus sin (A+B)

Rumus sinus jumlah dua sudut adalah sin (A+B) = sin A ∙ cos B + cos A ∙ sin B.

Pembuktian rumus sin (A+B) dapat ditunjukkan menggunakan identitas trigonometri lain yang sudah dibuktikan yaitu cos (A − B) = cos A ∙ cos B + sin A ∙ sin B, sin (90^o − A) = cos A, dan cos (90^o − A) = sin A.

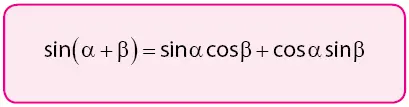
Pembuktian rumus sin (A+B) = sin A ∙ cos B + cos A ∙ sin B terdapat pada langkah-langkah berikut.

Bukti:
sin (A+B) = cos (90^o−(A+B))
= cos ((90^o−A) − B)
= cos (90^o−A)∙cos B + sin (90^o−A)∙sin B
= sin A ∙ cos B + cos A ∙ sin B

Baris terakhir menjadi bukti bahwa terdapat identitas trigonometri sin (A+B) = sin A ∙ cos B + cos A ∙ sin B (terbukti).

Contoh penggunaan rumus sin (A+B)

Soal:
Tentukan nilai dari sin 105^o ∙ cos 75^o + cos 105^o ∙ sin 75^o!

Jawab:
Sudut 105^o dan 75^o bukan merupakan sudut istimewa. Sementara jumlah dua sudut 105^o + 75^o = 180^o merupakan sudut istimewa.

Nilai fungsi trigonometri dengan besar sudut istimewa diketahui nilainya. Sehingga cara menetukan nilai dari sin 105^o ∙ cos 75^o + cos 105^o ∙ sin 75^o dapat menggunakan rumus sinus jumlah dua sudut sin (A+B).

sin 105^o ∙ cos 75^o + cos 105^o ∙ sin75^o
= sin (105^o + 75^o)
= sin 180^o
= 0

Jadi, nilai dari sin 105^o ∙ cos 75^o + cos 105^o ∙ sin 75^o = 0

Pembuktian rumus sin (A−B)

Rumus sinus selisih dua sudut adalah sin (A − B) = sin A ∙ cos B − cos A ∙ sin B.

Pembuktian rumus sin (A − B) dapat menggunakan identitas trigonometri lain yang sudah dibuktikan yaitu cos (A + B) = cos A ∙ cos B − sin A ∙ sin B, sin (90^o − A) = cos A, dan cos (90^o − A) = sin A.

Bagaimana pembuktian rumus sin (A − B) = sin A ∙ cos B − cos A ∙ sin B terdapat pada langkah-langkah berikut.

Bukti:
sin (A − B) = cos (90^o − (A − B))
= cos (90^o − A + B)
= cos ((90^o − A) + B)
= cos (90^o−A)∙cos B − sin(90^o−A)∙sin B
= sin A ∙ cos B − cos A ∙ sin B

Baris terakhir menjadi bukti bahwa terdapat identitas trigonometri sin (A − B) = sin A ∙ cos B − cos A ∙ sin B (terbukti).

Contoh Penggunaan Rumus Sin (A – B)

Soal:
Tentukan nilai dari sin 105^o cos 75^o + cos 105^o sin 75^o!

Jawab:
Diketahui bahwa 105^o dan 75^o bukan merupakan sudut istimewa. Sehingga nilai fungsi trigonometrinya hanya dapat diketahui dengan alat bantu kalkulator atau tabel.

Sedangkan selisih besar sudut 105^o − 75^o = 30^o merupakan sudut istimewa. Sehingga nilainya dapat diketahui tanpa alat bantu hitung atau tabel trigonometri. Dengan ini, rumus sinus selisih dua sudut dapat digunakan.

sin 105^o ∙ cos 75^o − cos 105^o ∙ sin 75^o
= sin (105^o − 75^o)
= sin 30^o
= ¹/₂

Jadi, nilai dari sin 105^o ∙ cos 75^o − cos 105^o ∙ sin 75^o = ¹/₂

Demikianlah tadi ulasan pembuktian rumus sin (A+B) atau rumus sinus jumlah dua sudut dan rumus sin (A−B) atau rumus sinus selisih dua sudut. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!