Arus listrik mengalir melalui kawat penghantar dalam suatu rangkaian listrik dengan arah dari kutub positif menuju kutub negatif. Dalam sebuah rangkaian listrik tidak sedikit yang dirangkai secara paralel sehingga memiliki percabangan. Besar kuat arus yang mengalir dalam percabangan dijelaskan melaui hukum Kirchoff 1 dan 2. Gustav Kirchhoff adalah seorang ilmuwan Jerman yang pertama kali menjelaskan bagaimana kuat arus, tegangan, dan hambatan listrik dalam suatu rangkaian listrik bercabang.
Apakah besarnya arus listrik pada setiap percabangan memiliki nilai yang sama? Bagaimana besar saat arus listrik menjumpai percabangan? Apa bunyi Hukum Kirchoff 1 dan 2? Bagaimana penerapan Hukum Kirchoff 1 dan 2? Sobat idschool dapat mencari tahu jawabannya melalui ulasan hukum Kirchoff 1 dan 2. di bawah.
Table of Contents
Baca Juga: Rumus Kuat Arus Listrik dalam Hukum Ohm pada Listrik Dinamis
Bunyi Hukum I Kirchoff
Hukum Kirchoff 1 dan 2 terdiri dari dua buah hukum yang menjelaskan bagaimana besar arus listrik dalam suatu rangkaian litstrik. Untuk hukum I Kirchhoff menjelaskan bagaimana persamaan besar arus listrik pada percabangan dalam rangkaian. Bunyi Hukum I Kirchhoff menyatakan bahwa jumlah kuat arus yang masuk pada setiap titik cabang sama dengan jumlah kuat arus yang keluar dari titik tersebut (∑Imasuk = ∑Ikeluar).

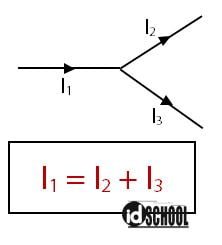
Sebagai contoh, arus listrik mengalir dari suatu kawat penghantar sebesar I1 A menuju sebuah percabangan dua kawat. Besarnya arus pada percabangan dua kawat tersebut adalah I2 A dan I3 A. Berdasarkan Hukum I Kirchhoff, persamaan yang terdapat pada rangkaian tersebut adalah I1 = I2 + I3.
Contoh penggunaan atau aplikasi Hukum I Kirchhoff untuk menyelesaikan suatu permasalahan pada rangkaian berikut.
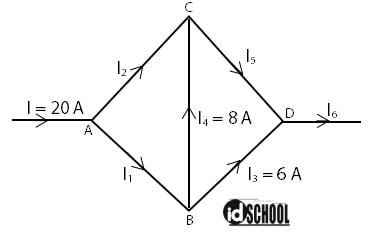
Pertanyaan:
Berapakah besar kuat arus yang mengalir pada I1, I2, I5, dan I6?
Penyelesaian:
Pertama, bentuk persamaan-persamaan berdasarkan Hukum I Kirchhoff sesuai rangkaian arus listrik yang diberikan pada soal.
- I = I1 + I2
- I1 = I4 + I3
- I5 = I2 + I4
- I6 = I5 + I3
Menghitung I1:
I1 = I4 + I3
I1 = 8 A + 6 A = 14 A
Menghitung I2:
I = I1 + I2
20 A = 14 A + I2
I2 = 20 A – 14 A = 6 A
Menghitung I5:
I5 = I2 + I4
I5 = 6 A + 8 A = 14 A
Menghitung I6:
I6 = I3 + I5
I6 = 6 A + 14 A = 20 A
Perhitungan untuk mendapatkan I6 juga dapat langsung menggunakan prinsip yang berlaku pada hukum I Kirchhoff. Karena arus yang masuk dalam rangkaian adalah 20 A maka arus yang keluar juga sama dengan 20 A.
Baca Juga: Cara Menghitung Biaya Pemakaian Listrik (+ Contoh Soal dan Pembahasan)
Bunyi Hukum Kirchoff II
Pemasangan rangkaian listrik pada kenyataannya melibatkan sistem rangkaian yang memuat lebih dari satu rangkaian atau loop. Penjelasan tentang tentang besar beda potensial yang mengitari suatu rangkaian tertutup dimuat dalam Hukum II Kirchhoff. Dasar dari hukum ini merupakan hukum kekekalan energi.
Bunyi Hukum II Kirchhoff menyatakan bahwa di dalam sebuah rangkaian tertutup, jumlah aljabar gaya gerak listrik (ε) dengan penurunan tegangan (IR) sama dengan nol.

Melalui Hukum II Kircchoff, persamaan beda potensial atau tegangan dalam sebuah sistem rangkaian listrik dapat dibentuk. Pembentukan persamaan dengan hukum II Kirchhoff perlu memperhatikan aturan-aturan berikut agar mempermudah prosesnya.
- Pilih rangkaian untuk masing-masing lintasan tertutup dengan arah tertentu.
- Arah loop dapat ditentukan secara bebas, usahakan memilih arah loop yang searah dengan arah arus listrik.
- Jika arah loop pada suatu cabang sama dengan arah arus maka penurunan tegangan bertanda positif.
- Jika arah loop berlawanan arah dengan arah arus maka penurunan tegangan bertanda negatif.
- Gaya gerak listrik bertanda positif jika saat mengikuti arah loop yang telah ditentukan menjumpai kutub sumber tegangan positif (kutub positif) terlebih dahulu
- Gaya gerak listrik bertanda negatif jika saat mengikuti arah loop yang telah ditentukan menjumpai kutub sumber tegangan negatif (kutub negatif) terlebih dahulu
Sebagai contoh, perhatikan penggunaan atau aplikasi Hukum Kirchoff 1 dan 2 untuk mengetahui kuat arus pada masing-masing penghambat dalam sebuah rangkaian listrik dua loop berikut.

Pertanyaan:
Berapakah besar arus listrik yang mengalir pada masing-masing hambatan?
Penyelesaian:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- E1 = 8 V
- R1 = 4 Ω
- E2 = 18 V
- R2 = 2 Ω
- R3 = 6 Ω
Langkah pertama yang perlu dilakukan adalah menentukan arah arus listrik dan loop. Langkah kedua selanjutnya membentuk persamaan yang sesuai Hukum Kirchoff 1 dan 2 seperti yang terdapat pada cara penyelesaian di bawah.

- Hubungan besar ketiga arus listrik: I3 = I1 + I2
- Loop I:
∑ε + ∑(I×R) = 0
–8 + 4I1 + 6I3 = 0
4I1 + 6I3 = 8
2I1 + 3I3 = 4
2I1 + 3(I1 + I2) = 4
2I1 + 3I1 + 3I2 = 4
5I1 + 3I2 = 4 →persamaan (1)
- Loop II:
∑ε + ∑(I×R) = 0
–18 + 2I2 + 6I3 = 0
2I2 + 6I3 = 18
I2 + 3I3 = 9
I2 + 3(I1+I2)= 9
I2 + 3I1 + 3I2 = 9
3I1 + 4I2 = 9 →persamaan (2)
Menghitung I1 dengan cara eliminasi I2 dari persamaan (1) dan (2):

Menghitung I2 dengan cara substitusi I1 = –1 A pada persamaan (1):
5×(–1) + 3I2 = 4
–5 + 3I2 = 4
3I2 = 9
I2 = 9/3 = 3 A
Menghitung I3 dengan cara substitusi I1 = –1 A dan I2 = 3 A pada persamaan I3:
I3 = I1 + I2
I3 = –1 + 3 = 2 A
Jadi, besar kuat arus (I) yang melalui hambatan R1, R2, dan R3 berturut-turut adalah I1 = 1 A, I2 = 3 A, dan I3 = 2A.
Baca Juga: 3 Bentuk Rangkaian Listrik (Seri, Paralel, dan Campuran)
Contoh Soal dan Pembahasan
Beebrapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan hukum Kirchoff 1 dan 2 di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana penggunaan hukum Kirchoff 1 dan 2. Sobat idschool dapat menggunakan pembahasan bagaimana penggunaan hukum Kirchoff 1 dan 2 sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Penerapan Hukum Kirchoff 1 dan 2

Bila besar I1 = I3 maka besar I4 adalah ….
A. 11 A
B. 7 A
C. 6 A
D. 3 A
Pembahasan:
Dari soal diketahui bahwa arus yang masuk adalah I1 dan I4, sementara arus yang keluar adalah I2, I3, dan I5. Sehingga dapat dibentuk persamaan sesuai hukum Kirchoff 1 yaitu I1 + I4 = I2 + I3 + I5. Dari soal diketahui juga bahwa besar arus I1 = I3 = 2 A, I2 = 3 A, dan I5 = 4 A.
Menghitung besar I4:
I1 + I4 = I2 + I3 + I5
2 + I4 = 3 + 2 + 4
2 + I4 = 9
I4 = 9 – 2 = 7 A
Jadi, Bila besar I1 = I3 maka besar I4 adalah 7 A.
Jawaban: B
Contoh 2 – Penerapan Hukum Kirchoff 1 dan 2
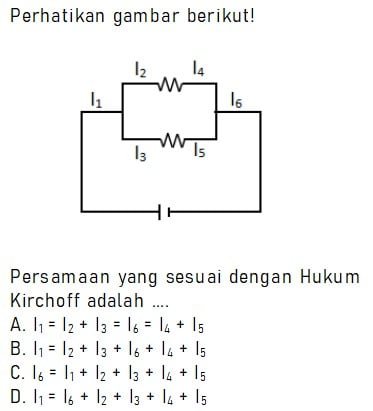
Pembahasan:
Dari gambar pada soal dapat diketahui bahwa besar arus listrik I1 sama dengan I6 (berdasarkan Hukum Kirchoff I). Sementara I2 = I3 dan I4 = I5 karena kedua arus berada dalam satu kawat penghantar yang lurus (tidak bercabang).
Dari Hukum Kirchoff I dapat disimpulkan bahwa I2 + I3 = I4 + I5. Jadi, persamaan yangs esuai dengan hukum Kirchoff adalah Bila besar I1 = I2 + I3 = I6 = I4 + I5.
Jawaban: A
Baca Juga: Cara Hitung Kuat Arus Listrik (I) di Setiap Titik pada Rangkaian Listrik 2 Loop dan 1 Loop
Contoh 3 – Penerapan Hukum Kirchoff 1 dan 2
Perhatikan gambar rangkaian listrik berikut ini!

Jika sumber tegangan mempunyai beda potensial 24 volt, kuat arus pada titik cabang I adalah ….
A. 1,2 A
B. 2,0 A
C. 2,4 A
D. 3,0 A
Pembahasan:
Berdasarkan informasi pada soal dapat diperoleh beberapa nilai besaran berikut.
- Sumber GGL: E = 24 Volt
- Hambatan dalam: r = 2 Ohm
- Resistor: R1 = 40 Ω, R2 = 20 Ω, dan R3 = 20 Ω
Menghitung hambatan pengganti pada rangkaian listrik.

Persamaan tegangan jepit:
V = E – I × r
V = 24 – 2I
Kuat arus pada titik cabang I :
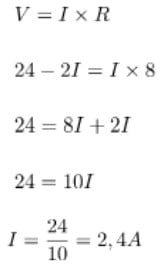
Sekian ulasan hukum Kirchoff 1 dan 2 yang meliputi bunyi hukum I Kirchoff dan hukum II Kirchoff beserta persamaan yang berlaku sesuai kedua hukum tersebut. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Besar Beda Potensial Antara Dua Titik
