Bentuk rumus integral fungsi trigonometri yang penting untuk diingat adalah ʃ sin x dx = cos x + C dan ʃ cos x dx = ‒sin x + C. Selain dua rumus integral fungsi trigonometri tersebut masih terdapat bebreapa rumus integral dari fungsi trigonometri lainnya. Rumus integral dari fungsi trigonometri berguna untuk menentukan hasil integral fungsi trigonometri yang cukup rumit seperti pada fungsi integral ʃ [sin2 (2x + 1) · cos (2x + 1)] dx.
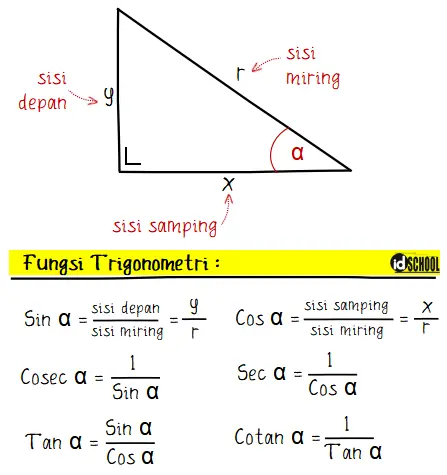
Fungsi trigonometri terdiri dari tiga fungsi darsar fungsi sinus (y = sin x) dan cosinus (y = cos x). Selain kedua fungsi dasar trigonometri tersebut juga terdapat fungsi lain seperti tangen (y = tan x = sin x/cos x), secan (y = 1/cos x), cosecan (y = 1/sin x), dan cotangen (y = 1/tan x). Fungsi trigonometri juga dapat berupa kombinasi beberapa fungsi trigonometri dasar, misalnya
Baca Juga: Rumus Turunan Fungsi Trigonometri +Contoh Soal +Pemabahsan
Penggunaan rumus integral fungsi trigonometri berguna untuk menentukan hasil integral dari fungsi-fungsi trigonometri. Apa saja rumus integral fungsi trigonometri? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Kumpulan Rumus Integral Fungsi Trigonometri
Rumus integral fungsi trigonometri diperoleh melalui definisi fungsi integral dan fungsi trigonometri. Dari gabungan dua definisi tersebut menghasilkan teorema yang dapat dianggap sebagai rumus integral dari fungsi trigonometri. Rumus dalam teorema-teorema fungsi integral trigonometri tersebut berbentuk hasil integral fungsi dasar yang dapat digunakan untuk menyelesaikan berbagai bentuk hasil integral dari fungsi trigonometri lainnya.
Beberapa rumus integral fungsi trignometri di bawah menjadi dasar untuk menyelesaikan berbagai bentuk integral fungsi trigonometri.
- ʃ sin x dx = ‒cos x + C
- ʃ cos x dx = sin x + C
- ʃ sec2x dx = tan x + C
- ʃ cosec2x dx = ‒cotan x + C
- ʃ (tan x)(sec x) dx = sec x + C
- ʃ (cotan x)(cosec x) dx = ‒cosec x + C
- ʃ tan x dx = ‒ln |cos x| + C
- ʃ cotan x dx = ln |sin x| + C
Selain beberapa rumus integral fungsi trigonometri bentuk dasar di atas, masih ada beberapa rumus lain yang dapat digunakan. Kumpulan rumus integral fungsi trigonometri yang dapat digunakan untuk mempermudah pengerjaan hasil integral dai fungsi trigonometri terdapat pada tabel di bawah.

Baca Juga: Nilai Minimum dan Maksimum Fungsi Trigonometri
2 Cara Menyelesaikan Hasil Integral Fungsi Trigonometri
Selain rumus integral fungsi trigonmetri, teknik pengintegralan yang tepat juga dibutuhkan dalam menyelesaikan hasil integral fungsi. Ada dua teknik yang dapat digunakan untuk menentukan hasil integral fungsi trigonometeri.
Kedua teknik yang dapat digunakan untuk menentukan hasil integral fungsi trigonometri adalah integral substitusi dan integral parsial.
1) Integral Substitusi
Substitusi dalam arti secara umum berarti penggantian. Dalam teknik integral substitusi berarti melakukan pemisalan variabel menjadi bentuk variabel lainnya.
Integral substitusi digunakan saat terdapat bagian sebuah fungsi yang merupakan fungsi lain.
Misalkan pada sebuah fungsi trigonometri f(x) = sin (3x + 5). Pemisalan variabel u = 3x + 5 akan membuat fungsi f(x) = sin (3x + 5) menjadi f(u) = sin u.
Dengan bentuk fungsi trigonometri f(u) = sin u akan lebih mudah untuk menentukan hasil fungsi integralnya. Di mana rumus integral fungsi trigonomeri untuk ʃ f(u) du = ʃ sin u du = −cos u + C.
Bagaimana cara menentukan hasil integral fungsi f(x) = sin (3x + 5) ditunjukkan seperti berikut.
Soal:
ʃ f(x) dx = ʃ sin (3x + 5) dx
Penyelesaian:
Misalkan,
u = 3x + 5
du/dx = 3 atau dx = du/3
ʃ sin (3x + 5) dx = ʃ sin u du/3
= −1/3 ʃ sin u du
= 1/3 · −cos u + C
= −1/3cos u + C
Selanjutnya perlu untuk melakukan substitusi kembali variabel u = 3x + 5 untuk mendapatkan hasil integral dari fungsi ʃ sin (3x + 5) dx. Sehingga akan diperoleh hasil integral fungsi ʃ sin (3x + 5) dx = 1/3 · cos (3x + 5) + C.
Contoh lain, teknik integral substitusi dapat juga digunakan untuk menentukan hasil integral fungsi berikut.
Soal:
ʃ (sin3x)(cos x) dx = . . . .
Hasil integral dari fungsi trigonometri pada soal di atas dapat diketahui melalui cara penyelesaian berikut.

2) Integral Parsial
Integral parsial digunakan saat terdapat perkalian dua fungsi. Di mana kedua fungsi tersebut memiliki derajat pangkat yang sama atau tidak bisa dijadikan turunan untuk fungsi lain.
Cara menentukan hasil integral dengan rumus integral parsial yaitu ∫u dv = uv − ∫v du. Contoh soal integral yang dikerjakan dengan rumus integral parsial adalah ∫ x · sin x dx.
Bagaimana cara menentukan hasil integral fungsi trigonometri ∫ x · sin x dx dilakukan seperti cara berikut.

Baca Juga: Cara Menentukan Nilai Limit Fungsi Trigonometri
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana penggunaan rumus integral fungsi trigonometri.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Integral Fungsi Trigonometri

Hasil integral fungsi trigonometri di atas adalah . . . .
A. ‒1/10 sin5 2x + C
B. ‒1/10 cos5 2x + C
C. ‒1/5 cos5 2x + C
D. 1/5 cos5 2x + C
E. 1/10 sin5 2x + C
Pembahasan:
Hasil integral dari fungsi trigonometri ∫ cos^42x sin 2x dx dapat dicari dengan metode integral substitusi.
Misalkan,
u = cos 2x
du = ‒2 sin 2x dx
dx = ‒du/2 sin 2x
Sehingga hasil integral dari fungsi ∫cos42x sin 2x dx dapat ditentukan dengan cara berikut.
∫cos42x·sin2x dx = ∫u4 sin2x · ‒du/2 sin 2x
= ‒1/2 ∫ u4 du
= ‒1/2 × 1/5 u5 + C
= ‒1/10 u5 + C
= ‒1/10 cos52x + C
Jadi, hasil integral fungsi trigonometri ∫cos42x·sin 2x dx = ‒1/10 cos52x + C.
Jawaban : B
Contoh 2 – Soal Integral Fungsi Trigonometri
∫ x2 cos ½x dx = . . . .
A. 4x sin ½x + 8 cos ½x + C
B. 4x sin ½x ‒ 8 cos ½x + C
C. 8 sin ½x + 4x cos ½x + C
D. 8 sin ½x ‒ 4x cos ½x + C
E. ‒8 sin ½x ‒ 4x cos ½x + C
Pembahasan:
Penentuan hasil integral pada soal di atas dapat dikerjakan dengan metode integral parsial. Pemisalan dilakukan untuk u = 2x dan dv = cos ½x, dengan langkah penyelesaian seperi berikut.
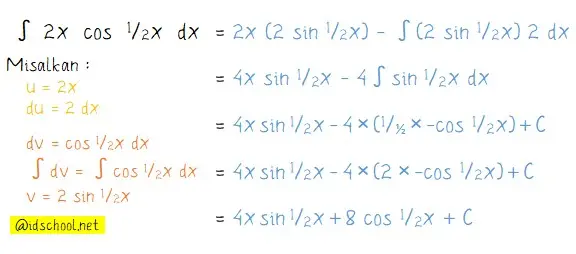
Jadi, hasil integral fungsi trigonometri ∫ x2 cos ½x dx = 4x sin ½x + 8 cos ½x + C.
Jawaban: A
Demikianlah tadi ulasan bagaimana rumus integral fungsi trigonometri dan contoh penggunaannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
