Hubungan kapasitas kapasitor (C), muatan (Q), dan energi (W) pada suatu rangkaian dengan tegangan V dapat dinyatakan dalam sebuah persamaan yaitu Q = CV dan W = ½CV2. Dari dua persamaan tersebut dapat disimpulkan bahwa besaran kapasitas kapasitor sebanding dengan jumlah muatan yang tersimpan di dalamnya. Dapat diperoleh kesimpulan juga bahwa energi yang tersimpan dalam kapasitor sebanding dengan kapasitas kapasitor.
Kapasitor atau yang sering juga disebut sebagai kondensator adalah alat yang memiliki fungsi untuk menyimpan muatan listrik atau energi listrik. Penggunaan kapasitor dapat ditemui pada alat-alat elektronik yang berperan sebagai penyimpan cadangan energi untuk digunakan ketika diperlukan.
Energi yang disimpan besarnya bergantung pada kapasitas kapasitor yang digunakan. Bagaimana cara menghitung kapasitas kapasitor? Bagaimana bentuk hubungan kapasitas kapasitor (C), muatan (Q), dan energi (W)? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Baca Juga: Rangkaian RLC (Resistor – Induktor – Kapasitor)
Table of Contents
- Rumus Kapasitas Kapasitor
- Hubungan Kapasitas Kapasitor (C), Muatan (Q), dan Energi (W) yang Dihasilkan
- Contoh Soal dan Pembahasan
Rumus Kapasitas Kapasitor
Sejumlah muatan atau energi yang mampu disimpan dalam suatu kapasitor disebut besaran kapasitansi atau kapasitas kapasitor. Satuan kapasitansi/kapasitas kapastitor dinyatakan dalam coloumb (C). Simbol kapasitor dalam sebuah rangkaian listrik berbentuk dua buah garis sejajar yang sama panjang (‒‒| |‒‒).
Bentuk kapasitor secara umum berupa dua pelat logam dengan letak sejajar dan berdekatan tetapi tidak saling bersentuhan. Besar kapasitas kapasitor bergantung pada jarak antara 2 pelat, luas pelat, dan medium dalam kapasitor.
Besar kapasitansi untuk kapasitor pelat sejajar dengan luas A, jarak keduanya d, dan antara pelat pada kapasitor hanya berisit udara sama dengan perkalian permitivitas listrik ruang hampa (ɛ0) dikali perbandingan luas dan jarak pelat.
Pada kapasitor dengan pelat yang diisi bahan dielektrik (isolator) dengan konstanta dielektrik K memiliki besar kapasitansi C = KC0. Bahan dielektrik adalah material yang dapat mempertahankan tegangan yang timbul pada permukaan yang diberi tegangan. Contoh bahan dielektrik adalah porselin, platik, kaca, karet, dsb.
Secara matematis, rumus kapasitansi dari kapasitor tanpa isi (hanya udara) dan dengan isi antara dua pelat sesuai dengan persamaan berikut.

Baca Juga: Besar Kuat Arus Listrik yang Mengalir dalam Suatua Rangkaian Listrik
Hubungan Kapasitas Kapasitor (C), Muatan (Q), dan Energi (W) yang Dihasilkan
Tegangan yang diberikan pada rangkaian kapasitor akan membuat kapasitor segera terisi muatan. Ada dua pelat pada kapasitor yang mana salah satu pelat menerima muatan positif dan yang satu lainnya memerima muatan negatif. Pengisian muatan pada kapasitor pada umumnya berlangsung singkat. Pengisian muatan kapasitor tidak ada dan tidak ada aliran arus listrik lagi saat kapasitor terisi muatan maksimum dan berada dalam keadaan tunak (steady state) atau konstan.
Jumlah muatan (Q) yang dapat tersimpan di dalam kapasitor sebanding dengan beda potensial (V) dan kapasitas kapasitor (C) atau Q = CV.
Sedangkan besarnya energi listrik yang tersimpan dalam kapasitor sama dengan usaha yang dilakukan untuk memindahkan muatan (Q) listrik dari sumber tegangan (V) ke dalam kapasitor. Bangun di bawah kurva pada grafik kapasitor dari keadaan kosong membentuk segitiga sehingga energi yang dihasilkan memenuhi perpersamaan W = ½QV. Substitusi nilai Q = CV ke persamaan akan menghasilkan persamaan baru untuk energi yang dihasilkan kapasitor yaitu W = ½ × Q × V = ½ × CV × V = ½CV2.
Sehingga, bentuk hubungan kapasitor (C), muatan (Q), dan energi (W) yang dihasilkan sesuai dengan persamaan-persamaan berikut.

Baca Juga: Contoh Cara Menghitung Biaya Pemakaian Listrik
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Kapasitas Kapasitor
Sebuah kapasitor mempunyai kapasitas sebesar 5 μF jika ada udara di antara keping-kepingnya, dan 30 μF jika antara keping-kepingnya ditempatkan lembaran porselen. Konstanta dielektrik porselen adalah ….
A. 0,17
B. 6
C. 25
D. 35
E. 150
Pembahasan:
Informasi pada soal memberikan keterangan beberapa besaran beserta nilainya seperti berikut.
- Kapasitas kapasitor antara dua pelat berbatas udara: C0 = 5 μF
- Kapasitas kapasitor antara dua pelat berbatas porselan: C = 30 μF
Menghitung konstanta dielektrik porselen (K):
C = K × C0
30 = K × 5
K = 30/5 = 6
Jadi, konstanta dielektrik porselen adalah 6.
Jawaban: B
Contoh 2 – Soal Kapasitas Kapasitor pada Rangkaian Gabungan
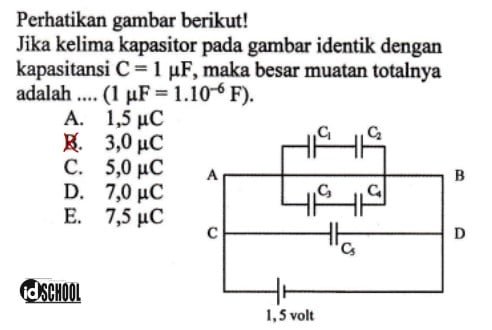
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh bebedapa informasi seperti berikut.
- Beda potensial dari rangkaian: V = 1,5 volt
- Rangkaian seri C1 dan C2 dirangkai paralel dengan rangkaian seri C3 dan C4
- Rangkaian C5 dirangkai paralel dengan empat kapasitor lainnya
- Kapasitas kapasitor: C1 = C2 = C3 = C4 = C5 = 1 μF = 1×10‒6 F = 10‒6 F
Menghitung kapasitansi ekivalen untuk beberapa kapasitor dengan rangkaian seri dan paralel (gabungan).

Menghitung muatan total (Q):
Q = Ctot × V
Q = 2·10-6 × 1,5
Q = 3×10-6 C = 3 μC
Jadi, besar muatan total dari rankaian tersebut sama dengan 3 μC.
Jawaban: B
Baca Juga: Rumus Energi dan Daya Listrik
Contoh 3 – Kapasitas Kapasitor
Sebuah kapasitor keping sejajar di udara mempunyai kapasitas C. Jika jarak kedua kepingnya diubah menjadi ½ kali semula dan kedua keping dicelupkan ke dalam medium dengan konstanta dielektrikum 2, kapasitasnya menjadi ….
A. ¼C
B. ½C
C. C
D. 2C
E. 4C
Pembahasan:
Beberapa keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Kapasitas kapasitor berisi udara: C0 = C
- Jarak kedua kepingnya diubah menjadi ½ kali semula: d1 = ½d
- Konstanta dielektrikum: K = 2
Menghitung kapasitas kapasitor setelah jarak diubah setengah kali semula dengan konstanta dielektrikum 2 (C1):
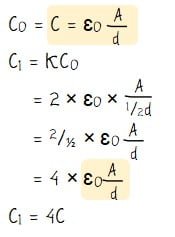
Jadi, jika jarak kedua kepingnya diubah menjadi ½ kali semula dan kedua keping dicelupkan ke dalam medium dengan konstanta dielektrikum 2 maka kapasitasnya menjadi 4C.
Jawaban: E
Contoh 4 – Soal Hubungan Kapasitas Kapasitor dengan Energi yang Disimpan
Dua buah kapasitor identik yang mula-mula belum bermuatan akan dihubungkan dengan baterai 10 V. Jika hanya salah satu yang dengan baterai tersebut, energi yang tersimpan dalam kapasitor adalah E. Energi yang akan tersimpan jika kedua kapasitor tersebut dihubungkan seri dengan baterai adalah ….
A. ¼E
B. ½E
C. E
D. 2E
E. 4E
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa informasi seperti berikut.
- Kapasitas dua kapasitor identik: C1 = C2 = C
- Tegangan baterai: V = 10 volt
- Energi yang tersimpan dalam sebuah kapasitor: W = ½CV2 = E
Persamaan untuk besar energi yang tersimpan pada sebuah kapasitor memenuhi E = ½CV2. Pada tegangan tetap maka besarnya energi sebanding dengan kapasitas kapasitor (E ~ C).
Ketika dua kapasitor dengan kapasitansi C dihubungkan seri maka kapasitansi ekivalen untuk dua kapasitor tersebut dapat dihitung seperti persamaan berikut.

Dengan demikian energi yang tersimpan pada rangkaian seri dari dua kapasitor yang dirangkai dengan baterai dengan tegangan yang sama dapat dicari seperti pada cara penyelesaian berikut.
W = ½CsV2
W = ½×C/2×V2
W = ½ × ½×C×V2
W = ½ × E = ½E
Jadi, energi yang akan tersimpan jika kedua kapasitor tersebut dihubungkan seri dengan baterai adalah ½E.
Jawaban: B
Demikianlah tadi ulasan kapasitas kapaitor yang besarnya dipengaruhi oleh luas pelat, jarak antara 2 pelat, isi antar pelat, dan bentuk rangkaian kapasitor. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Pengaruh Hambatan Kawat Penghantar Arus Listrik terhadap Besar Arus
