Rumus trigonometri jumlah dan selisih dua sudut adalah bentuk identitas trigonometri untuk penjumlahan/selisih dua sudut dari fungsi trigonometri. Untuk dua sudut A dan B dapat dibentuk identitas trigonometri fungsi sin (A+B), sin (A−B), cos (A+B), cos (A−B), tan (A+B), dan tan (A−B).
Identitas trigonometri untuk rumus jumlah pada fungsi sinus adalah sin (A+B) = sin A ∙ cos B + cos A ∙ sin B. Sedangkan identitas trigonometri rumus selisih dua sudut pada fungsi sinus adalah sin (A−B) = sin A ∙ cos B − cos A ∙ sin B.
Rumus jumlah dua sudut untuk fungsi cosinus adalah cos (A + B) = cos A ∙ cos B − sin A ∙ sin B. Dan rumus selisih dua sudut fungsi cosinus adalah cos (A − B) = cos A ∙ cos B + sin A ∙ sin B.
Untuk bentuk identitas rumus trigonometri jumlah dan selisih dua sudut untuk fungsi tangen dapat diperoleh dari perbandingan rumus trigonometri jumlah dan selisih dua sudut antara fungsi sinus dengan fungsi cosiunus.
Daftar isi:
Baca Juga: Nilai Minimum dan Maksimum Fungsi Trigonometri
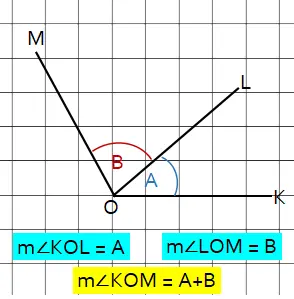
Rumus Trigonometri Jumlah Dua Sudut
Diketahui besar dua buah sudut adalah A dan B. Besar kedua sudut tersebut sama dengan A+B. Misalnya dua buah sudut diketahui memiliki besar A = 45o dan B = 60o. Besar jumlah dua sudut sama dengan C = 45o + 60o = 105o.
Besar sudut A = 45o dan B = 60o adalah dua sudut istimewa. Nilai fungsi trigonometri dari sudut istmewa dengan mudah dapat diketahui tanpa kalkulator.
Untuk besar sudut 105o bukan meruapkan sudut istimewa. Nilai fungsi trigonometri dengan besar sudut tersebut akan susah ditentukan jika tanpa bantuan kalkulator.
Selain dengan bantuan kalkulator, besar nilai fungsi trigonometri 105o dapat juga dihitung menggunakan rumus trigonometri jumlah dua sudut.
Ada tiga rumus trigonometri jumlah dua sudut:
- sin(A+B) = sin A ∙ cos B + cos A ∙ sin B
- cos(A+B) = cos A ∙ cos B − sin A ∙ sin B
- Fungsi tan jumlah dua sudut :
Bagaimana cara menggunakan rumus identitas trigonometri di atas terdapat pada pembahasan soal yang diberikan di akhir bagian.
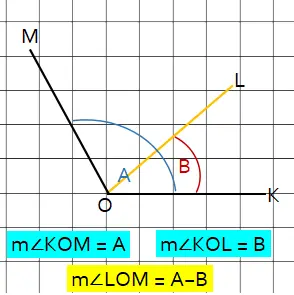
Rumus Trigonometri Selisih Dua Sudut
Besar dua buah sudut dapat juga dikurang dan mengahasilkan nilai selisih. Jumlah besar dua sudut A + B, maka selisih dua sudut menjadi A − B.
Ada tiga rumus trigonomerti selisih dua sudut:
- sin(A−B) = sin A ∙ cos B − cos A ∙ sin B
- cos(A−B) = cos A ∙ cos B + sin A ∙ sin B
- Fungsi tan selisih dua sudut:
Baca Juga: Turunan Fungsi Trigonometri
[Ringkasan] Rumus Trigonometri Jumlah dan Selisih Dua Sudut
Ada tiga rumus jumlah dua sudut fungsi trigonmetri. Ada tiga rumus selisih dua sudut fungsi trigonmetri. Sehingga ada enam rumus trigonometri jumlah dan selisih dua sudut. Keenam bentuk identitas rumus trigonometri jumlah dan selisih dua sudut terdapat pada tabel berikut.

Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Penggunaan rumus trigonometri jumlah dan selisih dua sudut
Dengan rumus trigonometri selisih dua sudut, maka nilai dari sin 15o adalah ….
Jawab:
Nilai sin 15o = sin (45o − 30o), sehingga nilai dari sin 15o dapat dicari dari rumus selisih dua sudut untuk fungsi sinus.
Rumus yang digunakan:
sin(A−B) = sin A ∙ cos B − cos A ∙ sin B
Diketahui beberapa nilai fungsi trigonometri dengan sudut istimewa berikut.
| Fungsi | 30o | 45o |
| sin | 1/2 | 1/2√2 |
| cos | 1/2√3 | 1/2√2 |
Cara mendapatkan nilai dari sin 15o dapat memanfaatkan nilai fungsi trigonometri dengan sudut istimewa di atas. Langkah perhitungan untuk mendapatkan nilai sin 15o terdapat pada langkah penyelesaian berikut.
sin 45o = sin (45o − 30o)
= sin 45o ∙ cos 30o − cos 45o ∙ sin 30o
= 1/2√2 ∙ 1/2√3 − 1/2√2 ∙ 1/2
= 1/4√6 − 1/4√2
= 1/4(√6 − √2)
Jadi, nilai dari sin 15o = 1/4(√6 − √2)
Baca Juga: Cara Menentukan Nilai Limit Fungsi Trigonmetri
Contoh 2 – Penggunaan rumus trigonometri jumlah dan selisih dua sudut
Dengan menggunakan rumus trigonometri jumlah dua sudut maka nilai tan 105o adalah ….
Jawab:
Nilai tan 105o = tan (60o + 45o), sehingga nilai dari tan 105o dapat dicari dari rumus jumlah dua sudut untuk fungsi tangen.
Cara menghitung nilai tan 105o terdapat pada langkah penyelesaian berikut.

Jadi, nilai tan 105o = −2 − √3
Demikianlah tadi ulasan rumus trigonometri jumlah dan selisih dua sudut. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Izin share bos, nilai tan 107 hasilnya negatif krn di kuadran II
Zakaria Kamal-X Tpm C/35
no comment