Fungsi kuadrat memiliki bentuk umum f(x) = ax2 + bx + c = 0 dengan a ≠ 0, contohnya adalah f(x) = 2x2 ‒ x ‒ 3. Dari nilai koefisien a, b, dan c menghasilkan beberapa sifat grafik fungsi kuadrat. Sifat-sifat grafik fungsi kuadrat dapat digunakan untuk mendapat gambaran bagaimana bentuk kurva secara cepat. Sebagai contoh, koefisien di depan x2 memberikan informasi bagaimana bentuk lengkungan kurva terbuka ke atas atau ke bawah.
Bentuk grafik fungsi kuadrat berupa parabola seperti huruf U atau huruf U yang terbalik. Titik balik kurva merupakan titik puncak yang koordinatnya (‒b/a, ‒D/4a). Di mana a adalah koefisien x2 dan b adalah koefisien x dari suatu persamaan kuadrat. Sementara D adalah diskriminan yang nilainya sama dengan D = b2 ‒ 4ac.
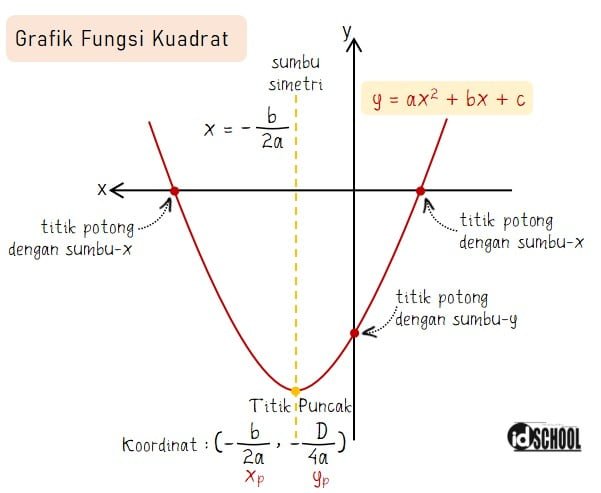
Baca Juga: Langkah-Langkah Menggambar Grafik Fungsi Kuadrat
Selain nilai a, nilai b dan c juga memengaruhi sifat grafik fungsi kuadrat. Apa saja sifat-sifat grafik fungsi kuadrat? Bagaimana bentuk sketsa grafik fungsi kuadrat? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- 1) Kurva Dapat Terbuka ke Atas atau Bawah
- 2) Kurva dapat Memotong Sumbu x pada 2 Titik, 1 Titik, atau Tidak Memotong Sumbu x
- 3) Grafik Fungsi Kuadrat Memotong Sumbu y Dapat Melalui 3 Cara
- 4) Letak Titik Balik Kurva Dapat Berada di Kanan, Tepat di Tengah, atau Kiri Sumbu y
- 5) Grafik Fungsi Kuadrat Berdasarkan Nilai a dan D
1) Kurva Dapat Terbuka ke Atas atau Bawah
Kurva dari suatu grafik fungsi kuadarat dapat terbuka ke atas dan ke bawah. Lengkung kurva tersebut dapat diketahui melalui nilai koefisien x2 dari suatu fungsi kuadrat. Untuk bentuk umum fungsi kuadrat f(x) = ax2 + bx + c, koefisien x2 adalah a.
Jika nila a lebih dari nol (a > 0) maka kurva akan terbuka ke atas. Jika nila a lebih kecil dari nol (a < 0) maka kurva akan terbuka ke bawah. Sementara untuk a sama dengan nol (a = 0) persamaan akan menjadi bentuk persamaan linear dan tidak masuk dalam bahasan persamaan kuadrat.
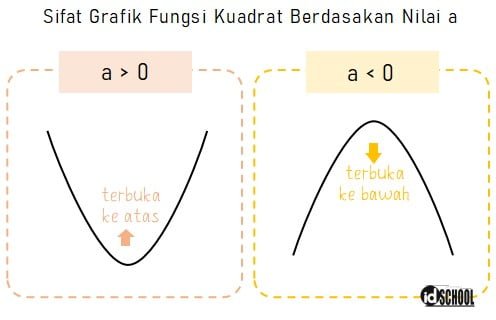
2) Kurva dapat Memotong Sumbu x pada 2 Titik, 1 Titik, atau Tidak Memotong Sumbu x
Kurva parabola dari fungsi kuadrat dapat memotong sumbu x di dua titik, satu titik, atau tidak memotong sumbu x. Banyaknya titik potong dengan sumbu x pada persamaan f(x) = ax2 + bx + c dapat diketahui melalui nilai diskriminan D = b2 ‒ 4ac.
Grafik fungsi kuadrat yang memotong sumbu x di satu titik memiliki nilai diskriminan D = 0. Untuk grafik fungsi kuadrat yang memotong sumbu x di dua titik memiliki nilai diskriminan D > 0. Sementara untuk kurva yang tidak memotong sumbu x memiliki nilai diskriminan D < 0.
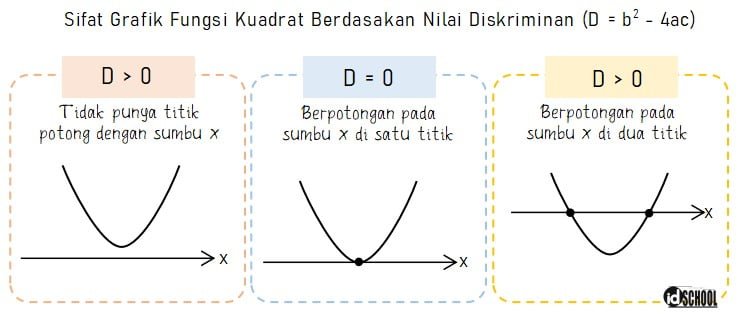
Baca Juga: Interval Fungsi Naik dan Turun
3) Grafik Fungsi Kuadrat Memotong Sumbu y Dapat Melalui 3 Cara
Untuk grafik fungsi kuadrat yang memotong sumbu y dapat terjadi di sumbu y positif, di titik O(0, 0), atau memotong di sumbu y negatif. Karakteristik ini dapat dilihat dari nilai c (konstanta) dari suatu persamaan kuadrat f(x) = ax2 + bx + c.
Kurva atau grafik fungsi kuadrat akan memotong sumbu y positif atau di atas sumbu x ketika nilai c > 0. Perpotongan kurva di titik O(0, 0) terjadi saat fungsi kuadrat memiliki c = 0. Dan kurva akan memotong sumbu y negatif atau di bawah sumbu x saat fungsi kuadrat memiliki c < 0.
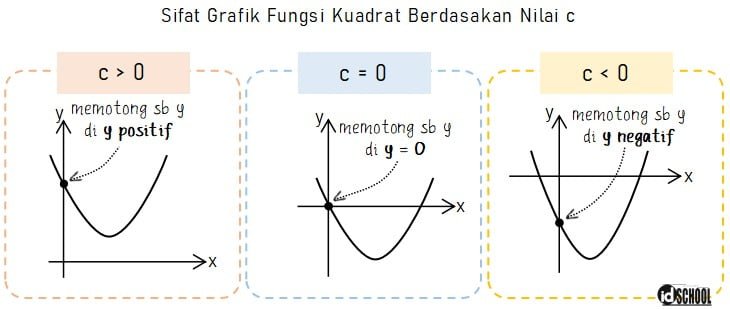
4) Letak Titik Balik Kurva Dapat Berada di Kanan, Tepat di Tengah, atau Kiri Sumbu y
Titik balik kurva merupakan titik puncak grafik fungsi kuadrat. Letak titik balik dapat berada di kanan, tengah, atau kiri sumbu y. Ketentuan untuk ketiga letak titik balik tersebut dapat dilihat berdasarkan nilai koefesien di depan x2 dan x. Untuk fungsi f(x) = f(x) = ax2 + bx + c, koefisien di depan x2 adalah a dan koefisien di depan x adalah b.
Titik balik kurva akan berada di kanan sumbu y saat b >< 0. Sementara, titik balik kurva akan berada di kiri sumbu y saat b >< 0.
Titik balik grafik fungsi kuadrat akan berada di titik O(0, 0) saat fungsi f(x) = ax2 + bx + c memiliki nilai b = 0. Contohnya adalah fungsi kuadrat dengan persamaan y = x2; f(x) = x2 ‒ 1; g(x) = x2 + 1; dan lain sebagainya.
Titik balik kurva untuk persamaan kuadrat f(x) = ax2 + bx + c yang memiliki bilangan a dan b dengan tanda sama berada di kiri sumbu y. Sementara titik balik untuk persamaan kuadrat f(x) yang memiliki bilangan a dan b berbeda tanda berada di kanan sumbu y. Untuk f(x) yang memiliki nilai b = 0 akan memiliki titik balik di titik O(0, 0).

Baca Juga: Cara Menentukan Persamaan Grafik Fungsi Kuadrat dari Sebuah Gambar
5) Grafik Fungsi Kuadrat Berdasarkan Nilai a dan D
Dari nilai a dan D = b2 ‒ 4ac pada fungsi kuadrat f(x) = ax2 + bx + c dapat diperoleh enam sketsa grafik fungsi kuadrat. Dari nilai a dapat diketahui bagaimana lengkungan kurva, apakah terbuka ke atas atau bawah. Sementara dari nilai D dapat diketahui banyak titik potong dengan sumbu x serta jenis akar-akar persamaan kuadrat apakah bilangan real atau imaginer.
Enam sketsa grafik fungsi kuadrat berdasarkan nilai a dan D dari persamaan kuadrat f(x) = ax2 + bx + c ditunjukkan seperti gambar berikut.

Saat nilai D < 0 terbentuk kurva yang nilainya akan selalu positif atau selalu negatif. Kondisi saat kurva yang menghasilkan nilai selalu positif disebut definit positif. Sedangkan kondisi saat kurva yang menghasilkan nilai selalu negatif disebut definit negatif.
Demikianlah tadi ulasan bagaimana sifat grafik fungsi kuadrat yang dapat diketahui melalui nilai koefisien-koefisien fungsi. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menentukan Persamaan Kuadrat Baru
