Sifat limit tak hingga dibutuhkan untuk menyelesaikan berbagai bentuk soal dengan fungsi limit yang didekati oleh suatu nilai yang sangat besar/kecil. Simbol untuk bilangan tak hingga adalah ∞ (infinity), dengan notasi nilai yang sangat besar +∞ dan nilai yang sangat kecil ‒∞. Untuk suatu nilai x yang mendekati nilai tak hingga pada suatu fungsi maka dituliskan x → ∞ atau x → ‒∞.
Nilai yang sangat besar jika terlibat operasi hitung oleh suatu nilai c akan menghasilkan nilai yang sangat besar. Sebagai contoh nilai yang sangat besar adalah 1.000.000.000.000.000 ditambah suatu nilai c = 1 maka akan menghasilkan nilai 1.000.000.000.000.001. Di mana hasil nilai tersebut juga merupakan bilangan yang sangat besar pula.
Bahasan untuk nilai tak hingga memiliki nilai yang lebih besar dari 1.000.000.000.000.000. Sehingga operasi hitung dengan nilai yang lebih kecil tidak begitu memengaruhi nilai tersebut.
Apa itu fungsi limit tak hingga? Apa saja sifat-sifat limit tak hingga? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Definisi Limit Tak Hingga
Limit dalam bahasan matematika menjelaskan sifat dari suatu fungsi jika mendekati suatu titik. Jika titik yang didekati adalah nilai yang sangat besar atau sangat kecil maka bahasan masuk dalam limit tak hingga.
Limit tak hingga adalah kajian untuk melihat bagaimana kecenderungan suatu fungsi jika nilai varibelnya sangat besar atau sangat kecil.
Definisi limit tak hingga sama seperti definisi limit yang didekati oleh suatu nilai. Hanya saja nilai yang mendekati fungsi adalah nilai yang sangat besar atau nilai yang sangat kecil. Sehingga definisi limit tak hingga sesuai dengan pernyataan berikut.

Baca Juga: 7 Tips untuk Menyelesaikan Soal Limit Fungsi
Sifat – Sifat Limit Tak Hingga
Dari definisi limit tak hingga dapat ditentukan suatu nilai limit fungsi yang didekati oleh nilai tak hingga. Dengan mengambil bentuk umum untuk beberapa fungsi sederhana maka dapat diperoleh beberapa sifat limit tak hingga. Beberapa sifat limit tak hingga dari suatu fungsi sederhana akan sangat berguna untuk menentukan nilai limit tak hingga dari fungsi yang lebih kompleks/rumit.
Ada dua bahasan sifat limit tak hingga yang perlu dibedakan agar dapat hasil lebih rinci yaitu sifat limit tak hingga fungsi aljabar dan fungsi trigonometri.
1) Limit Tak Hingga Fungsi Aljabar
Fungsi aljabar yang dapat berupa bentuk polinomial (pangkat), pecahan, penjumlahan, atau perkalian fungsi.
Hasil nilai tak hingga pada fungsi aljabar dapat terjadi jika suatu bilangan dibagi dengan bilangan nol. Sementara untuk suatu nilai yang dibagi oleh bilangan tak hingga akan menghasilkan nilai yang mendekati atau dianggap sama dengan nol.
Beberapa sifat limit tak hingga fungsi aljabar terdapat pada bentuk-bentuk berikut.

Selain sifat limit tak hingga, cara menentukan nilai limit tak hingga suatu fungsi juga membutuhkan teknik khusus. Beberapa teknik yang dapat digunakan untuk menentukan nilai limit tak hingga suatu antara lain membagi dengan pangkat tertinggi, mengalikan dengan akar sekawan, dan rumus cepat mengerjakan limit tak hingga.
Cara mengerjakan soal limit tak hingga dengan bentuk fungsi pecahan pada umumnya dilakukan dengan membagi dengan pangkat tertinggi. Untuk soal limit tak hingga dengan bentuk fungsi akar biasanya dikerjakan dengan mengalikan bentuk akar sekawan sehingga diperoleh bentuk pecahan variabel.
Sementara rumus cepat limit tak hingga hanya dapat digunakan untuk beberapa bentuk soal dengan kondisi tertentu.
2) Limit tak hingga fungsi trigonometri
Limit tak hingga fungsi trigonometri memiliki beberapa sifat fungsi limit tak hingga. Di mana sifat fungsi limit tak hingga fungsi trigonometri merupakan bentuk umum dari nilai-nilai yang sesuai dengan definisi limit tak hingga. Sehingga sifat-sifat limit tak hingga fungsi trigonometri dapat berguna untuk menentukan nilai limit tak hingga fungsi trigonometri dengan bentuk yang lebih rumit.
Limit fungsi trigonometri yang didekati oleh nilai yang sangat besar menghasilkan nilai yang tidak terdefinisi atau undefined. Hasil nilai tidak terdefinisi biasanya dituliskan ~ seperti pada limit fungsi f(x) = cos x dan f(x) = sin x yang didekati oleh nilai yang sangat besar/kecil.
Di mana nilai tidak terdefinisi tidak sama dengan nilai tidak terbatas, sebab tidak terdefinisi menunjuk nilai yang tidak ada (himpunan kosong). Sementara tidak terbatas menunjuk nilai yang sangat besar atau sangat kecil.
Beberapa sifat limit fungsi tak hingga fungsi trigonometri sesuai dengan persamaan-persamaan berikut.

Beberapa sifat limit tak hingga fungsi trigonometri di atas dapat membantu sobat idschool dalam mengerjakan berbagai bentuk soal. Selain itu, beberapa pengerjaan soal limit tak hingga fungsi trigonometri sering menggunakan fungsi bentuk-bentuk identitas trigonometri.
Bentuk identitas trigonometri digunakan agar bentuk soal memiliki kemiripan bentuk dengan sifat fungsi limit tak hingga fungsi trigonometri. Dengan demikian nilai limit fungsi dapat lebih mudah untuk ditentukan.
Baca Juga: 10++ Soal Limit Fungsi Trigonometri dan Pembahasannya
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Penggunaan Sifat Limit Tak Hingga
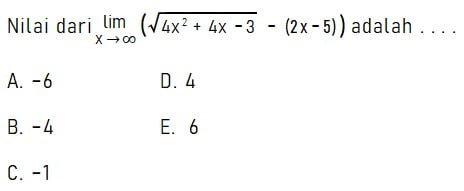
Pembahasan:
Nilai limit tak hingga untuk fungsi yang diberikan di atas dapat dikerjakan dengan dua cara. Cara pertama adalah pengerjaan dengan mengalikan fungsi dengan akar sekawan sehingga terdapat pecahan variabel x. Cara kedua dengan menggunakan rumus cepat limit tak hingga untuk bentuk-bentuk soal tertentu.
Cara pertama: mengalikan akar sekawan, kemudian membagi dengan pangkat tertinggi

Cara kedua: menggunakan rumus cepat limit tak hingga
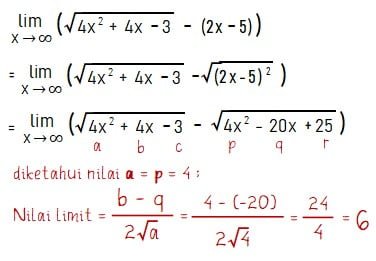
Dari kedua cara diperolah hasil yang sama yaitu 6, sobat idschool bisa memilih menggunakan cara pertama atau kedua. Jadi, nilai limit tak hingga dari fungsi pada soal tersebut adalah 6.
Jawaban: E
Contoh 2 – Penggunaan Sifat Limit Tak Hingga

Pembahasan:
Cara menentukan nilai limit tak hingga untuk bentuk fungsi seperti pada soal dilakukan dengan mengubah ke dalam bentuk yang lebih sederhana dengan pemfaktoran. Penyelesaian soal di atas ditunjukkan seperti cara berikut.

Jadi, nilai dari limit tak hingga fungsi tersebut adalah ‒5/2.
Jawaban: B
Contoh 3 – Penggunaan Sifat Limit Tak Hingga
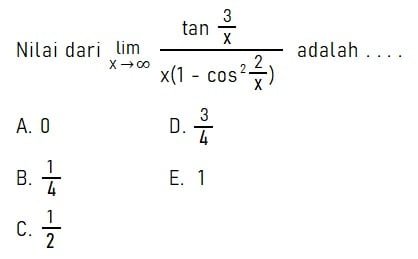
Pembahasan:
Untuk mengerjakan soal limit tak hingga di atas dibutuhkan pemisalan 1/x = y, sehingga untuk x → ∞ maka nilai y akan mendekati nol (y → 0). Selain itu dibutuhkan juga beberapa sifat limit yang didekati oleh nilai nol seperti pada penyelesaian soal limit tak hingga berikut.

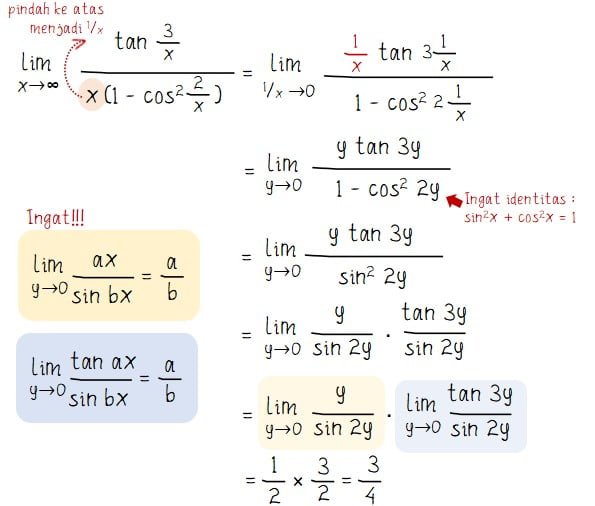
Jadi, nilai limit tak hingga untuk fungsi pada soal adalah 3/4.
Jawaban: D
Demikianlah tadi ulasan definisi dan sifat limit tak hingga yang disertai contoh penggunaannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
