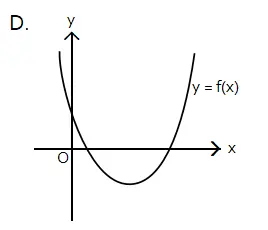Sketsa grafik fungsi kuadrat berguna untuk mengetahui bentuk grafik fungsi kuadrat secara cepat. Cara membuat sketsa grafik fungsi kuadrat dilakukan dengan mengamati nilai-nilai variabelnya. Apa saja yang diperhatikan dalam membuat sketsa grafik fungsi kuadrat ada di bawah.
Bentuk grafik fungsi kuadrat adalah kurva mulus berupa parabola. Kurva parobola yang dihasilkan dapat terbuka ke bawah atau terbuka ke atas. Banyak titik potong dengan sumbu x ada dua titik, satu titik, atau tidak memiliki titik potong.
Untuk titik potong dengan sumbu y dapat berada pada sumbu y positif, y = 0, atau sumbu y negatif. Titik puncak parabola dapat terletak di kanan sumbu y, kiri sumbu y, atau terletak pada sumbu y.
Daftar isi:
- Ketentuan Sketsa Grafik Fungsi Kuadrat
- Cara Membuat Sketsa Grafik Fungsi Kuadarat
- Contoh Soal dan Pembahasan
Ketentuan Sketsa Grafik Fungsi Kuadrat
Sketsa grafik fungsi kuadrat dapat dibuat berdasarkan nilai-nilai koefisien dan konstanta dari fungsi kuadrat. Bentuk umum fungsi kuadrat adalah f(x) = ax2 + bx + c. Nilai-nilai a, b, dan c dari fungsi f(x) digunakan untuk membuat sketsa parabola.
Ada empat ketentuan yang diperhatikan dalam membuat sketsa. Yaitu arah terbuka parabola, banyak titik potong dengan sumbu x, letak titik potong dengan sumbu y, dan letak titik balik maksimumnya.
- Nilai a menentukan arah terbuka parabola
- a > 0 → parabola terbuka ke atas
- a < 0 → parabola terbuka ke bawah
- a = 0 → grafik tidak berupa parabola
- Nilai diskriminan D = b2 – 4ac menentukan banyak titik potong kurva dengan sumbu x
- D > 0 → memiliki dua titik potong
- D = 0 → memiliki satu titik potong
- D < 0 → tidak memiliki titik potong
- Nilai c menentukan letak titik potong dengan sumbu y
- c > 0 → memotong sumbu y positif
- c = 0 → memotong sumbu y pada ordinat y = 0
- c < 0 → memotong sumbu y negatif
- Nilai ab menentukan letak koordinat titik balik kurva parabola
- ab > 0 → titik balik di kiri sumbu y
- b = 0 → titik balik terletak pada sumbu y
- ab < 0 → titik balik terletak di kanan sumbu y
Cara Membuat Sketsa Grafik Fungsi Kuadarat
Cara membuat sketsa grafik fungsi kuadrat ditunjukkan melalui contoh di bawah.
Soal:
Gambarlah sketsa grafik fungsi y = x2 – 2x – 8!
Pembahasan:
Persamaan y = x2 – 2x – 8 memiliki nilai a = 1, b = –2, dan c = –8.
Ketentuan 1: menentukan ke mana arah kurva parabola terbuka.
- Nilai a = 1
- Sehingga a > 0 → parabola terbuka ke atas
Ketentuan 2: mencari banyak titik potong kurva dengan sumbu-x.
Nilai diskriminan:
D = (–2)2 – 4(1)(–8)
D = 4 + 32 = 6
Nilai D > 0 sehingga kurva parabola memotong sumbu x pada dua titik.
Ketentuan 3: mengetahui letak titik potong dengan sumbu y.
- Nilai c = –8
- c < 0 sehingga kurva memotong sumbu y negatif
Ketentuan 4: letak titik balik atau titik puncak maksimum/minimum
- Diketahui a = 1 dan b = –2, maka ab = 1×(–2) = –2
- Untuk nilai ab < 0 → titik balik terletak di kanan sumbu y
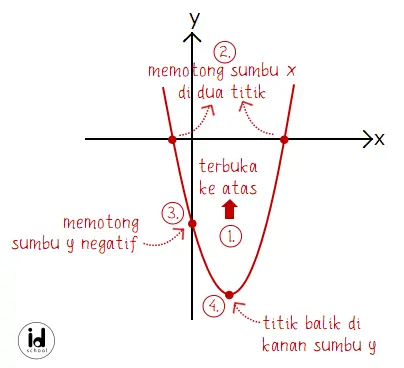
Kesimpulan yang diperoleh parabola terbuka ke atas, memotong sumbu x pada 2 titik, memotong sumbu y negatif, dan memiliki titik balik di kanan sumbu y.
Bentuk sketsa grafik fungsi yang sesuai untuk persamaan y = x2 – 2x – 8:
Baca Juga: 4 Langkah Menggambar Grafik Fungsi Kuadrat
Contoh Soal dan Pembahasan
Bentuk soal sketsa parabola dan pembahasannya ada di bawah.
Contoh Soal 1
Sketsa grafik fungsi kuadrat f(x) = 1/2x2 + x – 1 adalah ….
Pembahasan:
Dari persamaan fungsi kuadarat yang diberikan yaitu f(x) = 1/2x2 + x – 1 dapat diketahui nilai a = 1/2, b = 1, dan c = –1.
Menganalisis nilai-nilai variabelnya.
| Nilai variabel | Keterangan |
| a = 1/2 | a > 0 sehingga parabola terbuka ke atas |
| D = 12 – 4(1/2)(-1) D = 1 + 2 = 3 | D > 0 sehingga kurva memotong sumbu x di dua titik |
| ab = 1×(1/2) = 1/2 | ab > 0 sehingga letak titik balik kurva di kiri sumbu y |
| c = –1 | c < 0 maka kurva memotong sumbu y negatif |
Grafik fungsi kuadrat yang terbuka buka ke atas, memotong sumbu x di dua titik, memiliki letak titik balik di kiri sumbu y, dan memotong sumbu y negatif terdapat pada gambar di pilihan B.
Jadi, gambar sketsa grafik fungsi kuadrat f(x) = 1/2x2 + x – 1 sesuai pada pilihan B.
Jawaban: B
Contoh Soal 2
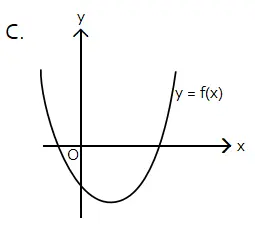
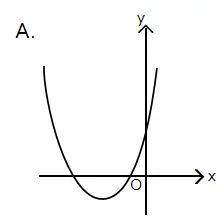
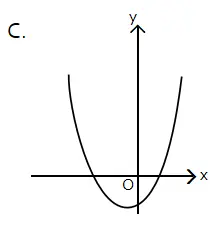
Sketsa grafik yang mungkin dari fungsi f(x) = ax2 + bx + c, dengan a > 0, b > 0, dan c < 0 adalah ….
Pembahasan:
Analisis nilai variabel untuk membuat sketsa parabola yang tepat ada di bawah.
| Nilai | Keterangan |
| a > 0 | parabola terbuka ke atas |
| ab > 0 | titik balik kurva berada di kiri sumbu y |
| c < 0 | memotong sumbu y negatif |
| D = (+)2 – 4(+)(–) = + (positif) | D > 0 sehingga kurva memotong sumbu x di dua titik |
Sketsa grafik fungsi kuadrat yang terbuka ke atas, titik balik berada di kiri sumbu y, memotong sumbu y negatif, dan memotong sumbu x di dua titik terdapat pada pilihan C.
Jawaban: C
Sekian ulasan cara membuat sketsa grafik fungsi kuadrat. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!