Definit negatif adalah suatu kondisi di mana fungsi kuadrat selalu memiliki nilai negatif. Sementara definit positif fungsi kuadrat adalah suatu kondisi di mana fungsi kuadrat selalu bernilai positif. Kondisi ini terjadi ketika fungsi kuadrat memiliki yang memiliki nilai diskriminan kurang dari nol (D = b2 – 4ac < 0).
Kurva dari fungsi kuadrat yang memiliki nilai diskriminan kurang dari nol tidak memiliki titik potong dengan sumbu x. Sehingga, fungsi kuadrat tidak memiliki akar-akar persamaan kuadrat.
Posisi kurva parabola dapat terletak di atas sumbu x (definit positif) dengan bentuk terbuka ke atas. Atau, posisi kurva parabola dapat terletak di bawah sumbu x (definit negatif) dengan bentuk terbuka ke bawah. Cari tahu lebih banyak mengenai definit positif dan negatif melalui ulasan di bawah.
Daftar isi:
Definit Positif Fungsi Kuadrat
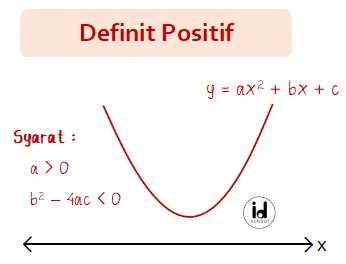
Definit positif fungsi kuadrat terjadi saat persamaan fungsi kuadarat memilki nilai diskriminan negatif dan nilai koefisien variabel pangkat tertingginya positif. Pada persamaan f(x) = x2 + bx + c, syarat definit positif fungsi kuadrat adalah a > 0 dan b2 – 4ac < 0.
Bentuk kurva parabola dari persamaan kuadrat yang memiliki nilai a > 0 dan b2 – 4ac < 0 adalah terbuka ke atas dan selalu berada di atas sumbu x. Kurva parabola ini dapat memiliki satu titik potong dengan sumbu y positif dan tidak memiliki titik potong dengan sumbu x. Letak titik puncak kurva dapat berada di kanan sumbu y atau di kiri sumbu y.
Gambaran kurva parabola yang memenuhi kondisi definit positif nampak seperti berikut.
Baca Juga: Ketentuan Cara Membuat Sketsa Grafik Fungsi Kuadrat
Definit Negatif Fungsi Kuadrat
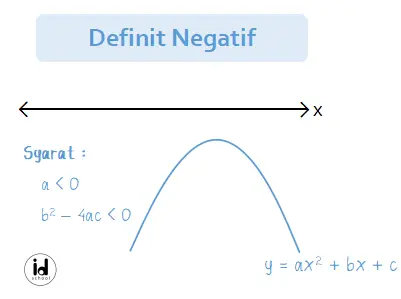
Definit negatif fungsi kuadrat terjadi saat persamaan fungsi kuadarat memilki nilai diskriminan negatif dan nilai koefisien variabel pangkat tertingginya negatif. Pada persamaan f(x) = x2 + bx + c, syarat definit positif fungsi kuadrat adalah a < 0 dan b2 – 4ac < 0.
Bentuk kurva parabola dengan nilai a < 0 dan b2 – 4ac < 0 adalah terbuka ke bawah dan selalu berada di bawah sumbu x. Kurva parabola dapat memiliki satu titik potong dengan sumbu y negatif dan tidak memiliki titik potong dengan sumbu x. Letak titik puncak kurva dapat berada di kanan sumbu y atau di kiri sumbu y.
Gambaran kurva parabola yang memenuhi kondisi definit negatif nampak seperti berikut.
Baca Juga: Cara Menentukan Persamaan Fungsi Kuadrat dari Gambar
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan soal dan pembahasan soal tersebut sebagai tolak ukur pemahaman materi di atas. Selamat Berlatih!
Soal 1
Fungsi kuadrat f(x) = px2 + 4x – 4 akan merupakan definit negatif, jika nilai p adalah ….
(A) p < –1
(B) p < 0
(C) p > 1
(D) –1 < p < 0
(E) p < –1 atau p > 0
Pembahasan:
Ada dua syarat yang harus dipenuhi suatu fungsi kuadrat agar memenuhi kondisi definit negatif yaitu nilai diskriminan D < 0 dan a < 0.
Nilai a pada fungsi kuadrat f(x) = px2 + 4x – 4 sama dengan p. Sehingga, nilai p harus kurang dari nol (p < 0) agar fungsi kuadrat tersebut merupakan definit negatif. Untuk p < 0 juga menghasilkan nilai determinan negatif (D < 0) sehingga syarat determinan agar fungsi kuadrat definit negatif akan terpenuhi.
Jadi, fungsi kuadrat f(x) = px2 + 4x – 4 akan merupakan definit negatif, jika nilai p adalah p < 0.
Jawaban: (B)
Soal 2
Fungsi f(x) = 2x2 – ax + 2 akan menjadi fungsi definit positif jika nilai a berada pada interval ….
(A) a > –4
(B) a > 4
(C) –4 < a < 4
(D) 4 < a < 6
(E) –6 < a < 4
Pembahasan:
Fungsi kuadrat f(x) = ax2 + bx + c memenuhi kondisi definit positif saat nilai a > 0 dan nilai diskriminan D < 0.
- Syarat definit postif:
- a > 0
- D = b2 – 4ac < 0
Pada fungsi kuadrat f(x) = 2x2 – ax + 2 telah memenuhi syarat nilai a > 0 agar fungsi kuadrat menjadi definit positif. Ada satu syarat lagi yang harus dipenuhi agar fungsi kuadrat f(x) = 2x2 – ax + 2 menjadi definit positif yaitu nilai diskriminan D < 0.
Menentukan nilai a:
(–a)2 – 4(2)(2) < 0
a2 – 16 < 0
(a – 4)(a + 4) < 0
Daerah a yang memenuhi:
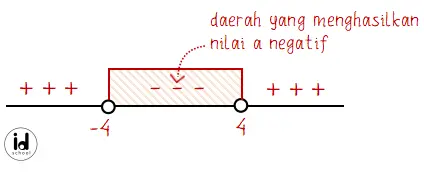
Jadi, fungsi f(x) = 2x2 – ax + 2 akan menjadi fungsi definit positif jika nilai a berada pada interval –4 < a < 4.
Jawaban: (C)
Demikianlah tadi ulasan apa itu definit negatif dan definit positif fungsi kuadrat. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Gambar Grafik Fungsi Kuadrat
