Suatu suku banyak f(x) dibagi x – 1 sisa 2, dibagi x ‒ 2 sisa 3. Suatu suku banyak g(x) dibagi x ‒ 1 sisa 5, dibagi x ‒ 2 sisa 4. Jika h(x) = f(x) ∙ g(x), maka sisa pembagian h(x) oleh x² ‒ 3x + 2 adalah ….
A. ‒2x + 12
B. ‒2x + 8
C. ‒x + 4
D. 2x + 8
E. x + 4

Jawab: D

Untuk menyelesaikan soal di atas dapat menggunakan teorema sisa yang berlaku pada pembagian suku banyak.

Misalkan Q(x) dan S(x) = ax + b berturut-turut adalah hasil bagi dan sisa hasil bagi dari suku banyak h(x) oleh x² ‒ 3x + 2. Berdasarkan teorema sisa, suku banyak h(x) akan memenuhi persamaan berikut.

h(x) = (x² ‒ 3x + 2) ∙ Q(x) + S(x)

h(x) = (x ‒ 2)(x ‒ 1) ∙ Q(x) + ax + b

Dari persamaan suku banyak h(x) = (x ‒ 2)(x ‒ 1) ∙ Q(x) + S(x) diketahui bahwa bentuk pembaginya adalah (x ‒ 2)(x ‒ 1). Sehingga dapat bentuk dua persamaan seperti berikut.

• Persamaan 1:
  • h(1) = S_f(x)(1) ∙ S_g(x)(1)
    
    (1 ‒ 2)(1 ‒ 1) ∙ H(1) + (a ∙ 1 + b) = 2 ∙ 5
    
    ‒1 ∙ 0 ∙ H(1) + a + b = 10
    
    a + b = 10

• Persamaan 2:
  • h(2) = S_f(x)(2) ∙ S_g(x)(2)
    
    (2 ‒ 2)(2 ‒ 1) ∙ H(2) + ( a ∙ 2 + b) = 3 ∙ 4
    
    0 ∙ 1 ∙ H(2) + 2a + b = 12
    
    2a + b = 12

Diperoleh dua persamaan yaitu a + b = 10 dan 2a + b = 12. Nilai a dan b dapat dicari menggunakan metode substitusi atau metode eliminasi pada penyelesaian sistem persamaan linear dua variabel (spldv).

Mencari nilai a:
Eliminasi b dari persamaan 1 dan 2.

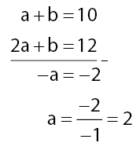
Mencari nilai b: substitusi nilai a = 2 pada persamaan a + b = 10 (atau 2a + b = 12).

2 + b = 10

b = 10 ‒ 2 = 8

Diperoleh nilai a = 2 dan b = 8, serta telah dimisalkan S(x) = ax + b. Sehingga sisa pembagian h(x) oleh x² ‒ 3x + 2 adalah S(x) = ax + b = 2x + 8.

Jadi, sisa pembagian h(x) oleh x² ‒ 3x + 2 adalah 2x + 8.