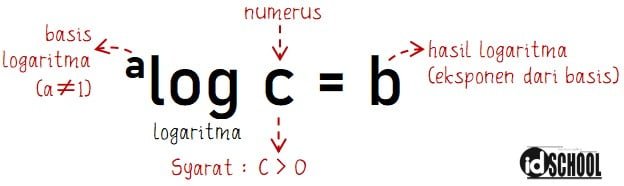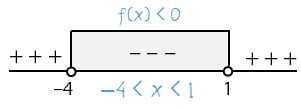Himpunan Penyelesaian Pertidaksamaan Logaritma (+Contoh Soal & Pembahasan)

Himpunan penyelesaian pertidaksamaan logaritma adalah nilai-nilai yang memenuhi suatu pertidaksamaan dari fungsi logaritma. Banyak nilai dalam himpunan bagian dapat terdiri dari satu, dua, atau tak hingga jumlahnya. Himpunan penyelesaian pertidaksamaan logaritma diperoleh dari hasil akhir perhitungan dengan mempertimbangkan syarat yang berlaku. Sehingga pengetahuan operasi hitung logaritma dasar g dalam menentukan himpunan penyelesaian pertidaksamaan logaritma.

Logaritma sendiri adalah sebuah fungsi kebalikan (fungsi invers) dari fungsi eksponen. Simbol logaritma ditulis dengan log yang disertai basis logaritma dan bilangan logaritma atau numerus. Persamaan umum logaritma dinyatakan dalam bentuk ^alog c = b atau log_a b = c. Di mana a = basis logaritma (a ≠ 1), b = hasil logaritma (eksponen dari basis) , dan c = bilangan logaritma (numerus). Syarat yang harus dipenuhi pada fungsi logaritma adalah nilai bilangan logaritma lebih dari 0 (numerus < 0). Nilai bilangan logaritma atau numerus yang kurang dari nol tidak akan mempunyai suatu hasil nilai yang sesuai.

Bagaimana cara menentukan himpunan penyelesaian pertidaksamaan logaritma? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Baca Juga: Cara Menggambar Grafik Fungsi Logaritma dan Bagaimana Menentukan Fungsi Logaritma dari Grafik yang Diberikan

Persamaan Logaritma

Persamaan logaritma adalah persamaan yang memuat fungsi logaritma. Tanda hubung persamaan logaritma sama seperti pada persamaan umum lainnya yaitu dihubungkan oleh sama dengan (=). Contoh persamaan logaritma adalah ²log 8 = 3, 2 log 10 = 2, y = ²log 8, dan lain sebagainya.

Pada contoh persamaan logaritma y = ²log 8 nilai y sama dengan 3. Hasil tersebut diperoleh dari definisi logaritma di mana jika y = ²log 8 maka 2^y = 8 yang dipenuhi ketika nilai y = 3.

Himpunan penyelesaian persamaan logaritma pada umumnya hanya memuat satu nilai yang memenuhi. Seperti pada contoh di atas misalnya, nilai yang memenuhi atau himpunan penyelesaian untuk persamaan y = ²log 8 adalah Hp = {3}.

Contoh lain dari persamaan logaritma:
Berapakah penyelesaian dari 2^{log x} = 1?

Penyelesaian:
2^{log x} = 1
2^{log x} = 2⁰
log x = 0
x = 10⁰ = 1

Jadi, himpunan penyelesian persamaan logaritma 2^{log x} = 1 adalah x = {1}.

Baca Juga: Berbagai Bentuk Persamaan Logaritma dan Cara Menyelesaikannya

Pertidaksamaan Logaritma

Bentuk pertidaksamaan logaritma berupa fungsi logaritma dengan tanda pertidaksamaan. Bentuk tanda pertidaksamaan dapat berupa kurang dari (<), lebih dari (>), kurang dari sama dengan (≤), atau lebih dari sama dengan (≥). Beberapa contoh pertidaksamaan logaritma diberikan seperti berikut.

• y ≤ ²log 8
• ²log²x + ²log x + 8 < 0
• log (x² – 11x + 22) > 1
• ³log(a² – b²) ≥ ³log(a – b)

Penyelesaian dari pertidaksamaan logaritma berupa beberapa nilai yang memenuhi pertidaksamaan. Misalnya pada contoh pertidaksamaan logaritma y ≤ ²log 8 dapat dipenuhi oleh y ≤ 3 → y = { … , 0, 1, 3}.

Penyelesaian:

y ≤ ²log 8
y ≤ ²log 2³
y ≤ 3 × ²log 2
y ≤ 3 × 1
y ≤ 3 → y ≤ {…, 0, 1, 3}

Baca Juga: Grafik Fungsi Eskponen dan Cara Menggambarnya

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idshcool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Himpunan Penyelesaian Persamaan Logaritma

Jika x₁ dan x₂ adalah akar-akar persamaan logaritma log(2x² – 11x + 22) = 1 maka nilai x₁·x₂ = ….
A. 11
B. 6
C. –¹/₂
D. –2
E. –5¹/₂

Pembahasan:

Penyelesaian persamaan logaritma:
log(2x² – 11x + 22) = 1
log(2x² – 11x + 22) = log 10
2x² – 11x + 22 = 10
2x² – 11x + 12 = 0

Diperoleh persamaan kuadrat 2x² – 11x + 12 = 0, di mana hasil kali akar-akar persamaan kuadrat secara umum (ax² – bx + c = 0) sama dengan ^c/_a. Dengan a adalah koefisien dari x² dan c adalah konstanta (bilangan tanpa variabel).

Nilai x₁·x₂ dari persamaan kuadrat 2x² – 11x + 12 = 0:
x₁·x₂ = ¹²/₂
x₁·x₂ = 6

Jawaban: B

Contoh 2 – Himpunan Penyelesaian Pertidaksamaan Logaritma

Penyelesaian pertidaksamaan ^x–2log (8–x) > 2 adalah ….
A. 3 < x < 4
B. –1 < x < 4
C. –4 < x < 1
D. x < 3 atau x > 4
E. x < –1 atau x > 4

Pembahasan:

Penyelesaian pertidaksamaan:

^x–2log (8–x) > 2 ↔ ^x–2log (8–x) > 2 · ^x–2log (2–x)
^x–2log (8–x) > ^x–2log (2–x)²
(8 – x) > (2 – x)²
8 – x > 4 – 4x + x²
x² – 4x + x + 4 – 8 < 0
x² – 3x – 4 < 0
(x + 4)(x – 1) < 0

Menentukan himpunan penyelesaian yang sesuai dengan pertidaksamaan.

Jadi, penyelesaian pertidaksamaan ^x–2log (8–x) > 2 adalah –4 < x < 1.

Jawaban: C

Contoh 3 – Himpunan Penyelesaian Pertidaksamaan Logaritma

Nilai x yang menjadi himpunan penyelesaian pertidaksamaan logaritma ^0,5log(x² – 3) > 0 adalah ….
A. –2<x<2
B. –2<x<–√3 atau √3<x<2
C. –2<x<2 atau x < √3
D. –2<x<√3
E. x<√3 atau x > 2

Pembahasan:

Nilai x yang menjadi himpunan penyelesaian pertidaksamaan logaritma harus memenuhi dua syarat. Pertama, nilai x memenuhi pertidaksamaan ^0,5log(x² – 3) > 0. Kedua, nilai x memenuhi pertidaksamaan x² – 3 > 0 (nilai numerus harus lebih dari 0).

• Syarat I:
  ^0,5log(x² – 3) > 0
  ^0,5log(x² – 3) > ^0,5log 1
  x² – 3 > 1
  x² – 4 > 0
  (x – 2)(x + 2) > 0

• Syarat II:
  x² – 3 > 0
  (x – √3)(x + √3) > 0

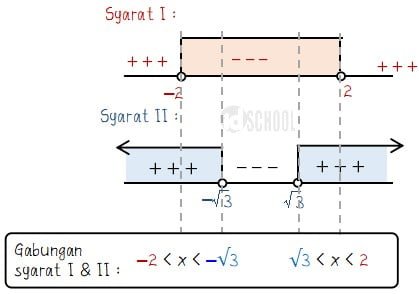
Menentukan himpunan penyelesaian pertidaksamaan logaritma:

Jadi, himpunan penyelesaian pertidaksamaan logaritma ^0,5log(x² – 3) > 0 adalah –2<x<–√3 atau √3<x<2.

Jawaban: B

Demikianlah tadi ulasan himpunan penyelesaian pesamaan logaritma dan himpunan penyelesaian pertidaksamaan logaritma. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Definisi dan 10 Sifat Logaritma