Kedudukan garis terhadap lingkaran menyatakan posisi sebuah garis lurus dengan persamaan y = mx + n terhadap suatu lingkaran dengan bentuk persamaan. Bentuk persamaan lingkaran dapat berupa x2 + y2 = r2, (x ‒ a)2 + (y ‒ b)2} = r2, atau x2 + y2 + Ax + By + C = 0. Kedudukan garis terhadap lingkaran meliputi tiga kondisi yaitu memotong lingkaran di dua titik, menyinggung lingkaran (memotong lingkaran pada satu titik), dan tidak memotong lingkaran.
Cara menentukan kedudukan garis dapat dilihat melalui gambar. Sayangnya, beberapa informasi hanya memberikan persamaan garis dan persamaan lingkaran tanpa meberikan gambaran detail kedua obyek tersebut. Sehingga perlu cara lain untuk mengetahui kedudukan garis terhadap lingkaran jika hanya diketahui persamaan garis dan persamaan lingkaran.
Bagaimana cara menentukan kedudukan garis terhadap lingkaran jika hanya diketahui persamaan garis dan persamaan lingkaran? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Cara Menentukan Kedudukan Garis Terhadap Lingkaran
Kedudukan garis terhadap lingkaran dapat diketahui melalui nilai diskrimnan dari persamaan kuadrat hasil substitusi persamaan garis ke persamaan lingkaran. Ingat kembali sedikit materi tentang persamaan kuadrat, di mana sebuah persamaan kuadrat memiliki pangkat tertinggi 2 (dua).
Bentuk umum persamaan kuadrat dinyatakan melalui persamaan ax2 + bx + c = 0. Nilai diskriminan (D) dari bentuk umum persamaan kuadrat tersebut dapat diperoleh melalui persamaan D = b2 ‒ 4ac.
Persamaan kuadrat: ax2 + bx + c = 0
Diskriminan: D = b2 ‒ 4ac
Misalkan sebuah garis diketahui memiliki persamaan y = mx + n dan sebuah lingkaran memiliki persamaan x2 + y2 + Ax + By + C = 0. Substitusi persamaan garis ke persamaan lingkaran akan menghasilkan sebuah persamaan kuadrat dalam variabel x seperti berikut.
x2 + (mx + n)2 + Ax + B(mx + n) + C = 0
x2 + m2x2 + 2mnx + n2 + Ax + Bmx + Bn + C = 0
(m2 + 1)x2 + (2mn + Bm + A)x + n2 + Bn + C = 0
Diperoleh sebuah persamaan dengan a = m2 + 1, b = 2mn + Bm + A, dan c = n2 + Bn + C. Dengan nilai a, b, dan c tersebut kemudian dapat ditentukan nilai diskriminan D. Selanjutnya dari nilai D dapat diselidiki bagaimana kedudukan garis terhadap lingkaran.
Baca Juga: Kedudukan Antara 2 lingkaran
1) Garis memotong lingkaran pada dua titik
Garis yang memotong lingkaran pada 2 titik berarti memiliki dua buah titik koordinat yang sama. Dua koord Gambar kedudukan garis terhadap lingkaran yang berpotongan pada dua titik dapat dilihat pada gambar di bawah.

Kedudukan garis yang memotong dua titik pada lingkaran dapat terjadi jika nilai D > 0 atau b2 ‒ 4ac > 0.
D > 0 ↔ b2 ‒ 4ac > 0
garis memotong lingkaran di 2 titik
Baca Juga: Cara Menentukan Persamaan Lingkaran yang Melalui 3 Titik
2) Garis menyinggung lingkaran (berpotongan pada satu titik)
Contoh kedudukan garis terhadap lingkaran yang menyinggung lingkaran dapat dilihat pada gambar di bawah.
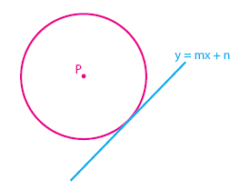
Kedudukan garis yang memotong satu titik pada lingkaran (menyinggung lingkaran) dapat terjadi jika nilai D = 0.
D = 0 ↔ b2 ‒ 4ac = 0
garis memotong lingkaran pada 1 titik (menyinggung lingkaran)
3) Garis tidak memotong lingkaran
Selanjutnya adalah kondisi yang ketiga, yaitu posisi garis dan lingkaran saling lepas, atau dapat dikatakan bahwa garis tidak memotong lingkaran. Ilustrasinya dapat dilihat pada gambar di bawah.
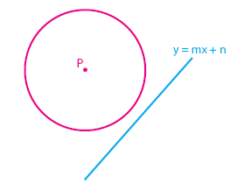
Kedudukan garis yang tidak memotong lingkaran (tidak memiliki titik perpotongan atau persinggungan) dapat terjadi jika nilai D < 0.
D < 0 ↔ b2 ‒ 4ac < 0
garis dan lingkaran saling lepas (garis tidak memotong lingkaran)
Baca Juga: Kedudukan Titik Terhadap Lingkaran
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Kedudukan Garis Terhadap Lingkaran
Soal:
Tentukan kedudukan garis g: 5x + 2y – 4 = 0 terhadap lingkaran x2 + y2 = 5!
Pembahasan:
Langkah pertama substitusi variabel y dari persamaan garis g: 5x + 2y – 4 = 0 ke persamaan lingkaran x2 + y2 = 5 sehingga diperoleh suatu persamaan kuadrat. Sehingga perlu untuk mencari persamaan variabel y dari garis 5x + 2y – 4 = 0 terlebih dahulu.
Menentukan persamaan y:
5x + 2y – 4 = 0
2y = –5x + 4
y = –5/2x + 4/2
y = –5/2x + 2
Substitusi persamaan y = –5/2x + 2 ke persamaan lingkaran x2 + y2 = 5 seperti yang dilakukan pada cara berikut.
x2 + y2 = 5
x2 + (–5/2x + 2)2 = 5
x2 + (25/4x2 – 10x + 4) = 5
x2 + 25/4x2 – 10x + 4 = 5
Kalikan kedua ruas dengan bilangan 4 untuk mempermudah perhitungan:
4x2 + 25x2 – 40x + 16 = 20
29x2 – 40x + 16 – 20 = 0
29x2 – 40x – 4 = 0
Diperolah a = 29, b = –40, dan c = –4 yang selanjutnya dapat digunakan untuk menghitung nilai diskriminan.
Menghitung nilia diskriminan D:
D = b2 – 4ac
D = (–40)2 – 4×29×(–4)
D = 1.600 – (–464)
D = 1.600 + 464 = 2.064
Dari hasil perhitungan diperoleh kesimpulan bahwa D > 0 sehingga garis g: 5x + 2y – 4 = 0 memotong lingkaran x2 + y2 = 5 pada dua titik.
Contoh 2 – Soal Kedudukan Garis Terhadap Lingkaran
Soal:
Selidiki kedudukan garis y = 2/3x – 3 pada lingkaran dengan persamaan x2 + y2 + 6x – 12y – 19 = 0!
Pembahasan:
Pertama, substitusi persamaan garis y = 2/3x – 3 pada lingkaran x2 + y2 + 6x – 12y – 19 = 0 seperti yang ditunjukkan melalui cara berikut,
x2 + y2 + 6x – 12y – 19 = 0
x2 + (2/3x – 3)2 + 6x – 12(2/3x – 3) – 19 = 0
x2 + (4/9x2 – 2 × 2/3x × 3 + 9) + 6x – 8x + 36 – 19 = 0
x2 + 4/9x2 – 4x + 9 + 6x – 8x + 36 – 19 = 0
13/9x2 – 4x + 6x – 8x + 9 + 36 – 19 = 0
13/9x2 – 6x + 26 = 0
Berdasarkan persamaan kuadrat di atas diperoleh nilai a, b, dan c seperti berikut.
a = 13/9
b = –6x
c = 26
Nilai diskriminan (D) dari persamaan kuadrat 13/9x2 – 6x + 26 = 0 dapat dihitung seperti yang ditunjukkan cara berikut.
D = b2 – 4ac
D = (–6)2 – 4(13/9)(26)
D = 36 – 1.352/9
D = 324/9 – 1.352/9
D = –1.028/9
Karena nilai D = –1.028/9 < 0, maka garis tersebut saling lepas dengan lingkaran atau tidak memotong lingkaran.
Sekian ulasan tentang kedudukan garis terhadap lingkaran yang meliputi garis memotong lingkaran pada 2 titik, menyinggung lingkaran, dan tidak memotong lingkaran. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
